网址：http://m.1010jiajiao.com/timu_id_35373[举报]
一、选择题 BDACA BCBCD
二、填空题
11．4 12. 2 13. 答案不唯一(如:y=x+1,y=x-3…等等.) 14. 107
15. 
16.
35 17. 10 18. 18
三、解答题
19．由（1）与（2）组成的代数的和（选择其他组合可参照本题标准给分）.
+
…………………………（1分）
…………………………（4分）
…………………………（6分）
…………………………（8分）
…………………………（10分）
注: 代数式（1）与（3）的和为
；代数式（2）与（3）的和为
.
20．（1）画图正确. ………………………………（3分）
（2）316, 165, 38.6(或38.4), 139, 13.6(或13.4) …………………（8分）
21．设该公司招聘软件推销人员为x人，软件设计人员为y人， ………（1分）
依题意，得 
……………………（6分）
解这个方程组，得 
…………………………（9分）
答：该公司招聘软件推销人员为50人，软件设计人员为70人. ……（10分）
（注：其他解法参照上述标准给分.）
22．所画的两个图案中,有一个图案只是轴对称(或只是中心对称)的给4分,另一个图案既是轴对称图形又是中心对称图形的给6分.答案不唯一,以下设计图案仅供参考.
23.（1）∵ 四边形ABCD是正方形，BD是对角线，且MN∥DC，
∴ 四边形AMNB和四边形MNCD都是矩形，
△MED和△NBE都是等腰直角三角形.
∴ ∠AME=∠ENF=90°，AM=BN=NE. …………………………（3分）
∴ ∠EFN+∠FEN=90°. …………………………（4分）
又∵ EF⊥AE，
∴ ∠AEM+∠FEN=90°， …………………………（5分）
∴ ∠EFN=∠AEM ， …………………………（6分）
∴ △AME≌△ENF. …………………………（7分）
（2）四边形AFNM的面积没有发生变化. …………………………（8分）
（?）当点E运动到BD的中点时，
四边形AFNM是矩形，S四边形AFNM=
. ………………（9分）
（?）当点E不在BD的中点时，点E在运动（与点B、D不重合）的过程中，四边形AFNM是直角梯形.
由（1）知，△AME≌△ENF.
同理，图12.2中，△AME≌△ENF.
∴ ME=FN，AM=EN.
∴ AM+FN=MN=DC=1. …………………………（11分）
这时 S四边形AFNM=(AM+FN)?DC=?1?1=.
综合（?）、（?）可知四边形AFNM的面积是一个定值. …………（12分）
24．（1）∵ 抛物线
经过O(0,0)，A(4,0),B(3,
)，
∴ 
.解得 
. ………（2分）
∴ 所求抛物线的函数关系式为
. ………………（3分）
(注：用其它方法求抛物线的函数关系式参照以上标准给分.)
（2）① 过点B作BE⊥
轴于E，则BE=，AE=1，AB=2.
由tan∠BAE=
，得∠BAE =60°.
…………（4分）
（?）当点Q在线段AB上运动，即0＜
≤2时，QA=t，PA=4-.
过点Q作QF⊥轴于F，则QF=
，
∴ S=PA?QF
. ……（6分）
（?）当点Q在线段BC上运动，即2≤＜4时，Q点的纵坐标为，PA=4-.
这时，S=
.
……………………（8分）
②（?）当0＜≤2时，
.
∵ 
，∴ 当=2时，S有最大值，最大值S=. ……（9分）
（?）当2≤＜4时，
∵ 
， ∴ S随着的增大而减小.
∴ 当=2时，S有最大值，最大值
.
综合（?）（?），当=2时，S有最大值，最大值为. ……（10分）
△PQA是等边三角形. …………………………（11分）
③ 存在. …………………………（12分）
当点Q在线段AB上运动时，要使得△PQA是直角三角形，必须使得∠PQA =90°，这时PA=2QA，即4-=2，∴ 
.
∴ P、Q两点的坐标分别为P1(
,0)，Q1(
,
). ……（13分）
当点Q在线段BC上运动时，Q、P两点的横坐标分别为5-和，要使得△PQA是直角三角形，则必须5-=，∴ 
∴ P、Q两点的坐标分别为P2(
,0)，Q2(,). ………………（14分）
(注：用其它方法求解参照以上标准给分.)
（本题满分12分）
已知直角坐标系中菱形ABCD的位置如图，C，D两点的坐标分别为(4,0)，(0,3).现有两动点P,Q分别从A,C同时出发，点P沿线段AD向终点D运动，点Q沿折线CBA向终点A运动，设运动时间为t秒.
1.(1)填空：菱形ABCD的边长是 ▲ 、面积是 ▲ 、 高BE的长是 ▲ ；
2.(2)探究下列问题：
若点P的速度为每秒1个单位，点Q的速度为每秒2个单位.当点Q在线段BA上时
② △APQ的面积S关于t的函数关系式，以及S的最大值；
3.（3）在运动过程中是否存在某一时刻使得△APQ为等腰三角形，若存在求出t的值；若不存在说明理由.
查看习题详情和答案>>
已知菱形ABCD的边长为1．∠ADC=60°，等边△AEF两边分别交边DC、CB于点E、F。
【小题1】（1）特殊发现：如图1，若点E、F分别是边DC、CB的中点．求证：菱形ABCD对角线AC、BD交点O即为等边△AEF的外心；
【小题2】（2）若点E、F始终分别在边DC、CB上移动．记等边△AEF的外心为点P．
①猜想验证：如图2．猜想△AEF的外心P落在哪一直线上，并加以证明；
②拓展运用：如图3，当△AEF面积最小时，过点P任作一直线分别交边DA于点M，交边DC的延长线于点N，试判断
是否为定值．若是．请求出该定值；若不是．请说明理由。
查看习题详情和答案>>
已知直角坐标系中菱形ABCD的位置如图，C，D两点的坐标分别为(4,0)，(0,3).现有两动点P,Q分别从A,C同时出发，点P沿线段AD向终点D运动，点Q沿折线CBA向终点A运动，设运动时间为t秒.
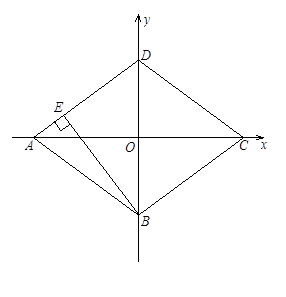
【小题1】(1)填空：菱形ABCD的边长是 ▲ 、面积是 ▲ 、 高BE的长是 ▲ ；
【小题2】(2)探究下列问题：
若点P的速度为每秒1个单位，点Q的速度为每秒2个单位.当点Q在线段BA上时
② △APQ的面积S关于t的函数关系式，以及S的最大值；
【小题3】（3）在运动过程中是否存在某一时刻使得△APQ为等腰三角形，若存在求出t的值；若不存在说明理由. 查看习题详情和答案>>
是否为定值．若是．请求出该定值；若不是．请说明理由。
