网址:http://m.1010jiajiao.com/timu_id_329050[举报]
某校从参加某次知识竞赛的同学中,选取60名同学将其成绩(百分制)(均为整数)分成6组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题.
(Ⅰ)求分数在[70,80)内的频率,并补全这个频率分布直方图;
(Ⅱ)从频率分布直方图中,估计本次考试的平均分;
(Ⅲ)若从60名学生中随机抽取2人,抽到的学生成绩在[40,70)记0分,在[70,100]记1分,用X表示抽取结束后的总记分,求X的分布列和数学期望.
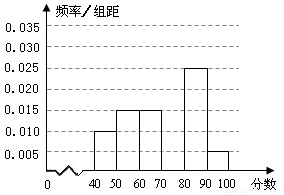
【解析】第一问中设分数在[70,80)内的频率为x,根据频率分布直方图,则有
(0.01+0.015×2+0.025+0.005)×10+x=1,可得x=0.3,
第二问平均分为:
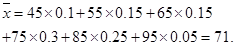
第三问学生成绩在[40,70)的有0.4×60=24人,
在[70,100]的有0.6×60=36人,并且X的
可能取值是0,1,2.
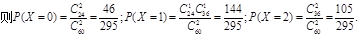
查看习题详情和答案>>
(1)通过抽签将他们安排到1~4号靶位,试求恰有2名运动员所抽靶位号与其参赛号码相同的概率;
(2)记1号、2号射箭运动员射箭的环数为ξ(ξ所有取值为0,1,2,3,…,10)分别为P1,P2.根据教练员提供的资料,其概率分布如下表:
| ξ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| P1 | 0 | 0 | 0 | 0 | 0.06 | 0.04 | 0.06 | 0.3 | 0.2 | 0.3 | 0.04 |
| P2 | 0 | 0 | 0 | 0 | 0.04 | 0.05 | 0.05 | 0.2 | 0.32 | 0.32 | 0.02 |
②判断1号、2号射箭运动员谁射箭的水平高?并说明理由.
(1)通过抽签将他们安排到1~4号靶位,试求恰有一名运动员所抽靶位号与其参赛号码相同的概率;
(2)记1号,2号射箭运动员,射箭的环数为ξ(ξ所有取值为0,1,2,3…,10).
根据教练员提供的资料,其概率分布如下表:
| ξ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| P1 | 0 | 0 | 0 | 0 | 0.06 | 0.04 | 0.06 | 0.3 | 0.2 | 0.3 | 0.04 |
| P2 | 0 | 0 | 0 | 0 | 0.04 | 0.05 | 0.05 | 0.2 | 0.32 | 0.32 | 0.02 |
②判断1号,2号射箭运动员谁射箭的水平高?并说明理由. 查看习题详情和答案>>
(12分)在奥运会射箭决赛中,参赛号码为1~4号的四名射箭运动员参加射箭比赛。
(Ⅰ)通过抽签将他们安排到1~4号靶位,试求恰有两名运动员所抽靶位号与其参赛号码相同的概率;
(Ⅱ)记1号、2号射箭运动员射箭的环数为![]() (
(![]() 所有取值为0,1,2,3...,10)分别为
所有取值为0,1,2,3...,10)分别为![]() 、
、![]() .根据教练员提供的资料,其概率分布如下表:
.根据教练员提供的资料,其概率分布如下表:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 0 | 0 | 0 | 0 | 0.06 |
| 0.06 | 0.3 | 0.2 | 0.3 | 0.04 |
| 0 | 0 | 0 | 0 | 0.04 |
|
| 0.2 | 0.32 | 0.32 | 0.02 |
![]()
①若1,2号运动员各射箭一次,求两人中至少有一人命中9环的概率;
②判断1号,2号射箭运动员谁射箭的水平高?并说明理由. 查看习题详情和答案>>在奥运会射箭决赛中,参赛号码为1~4号的四名射箭运动员参加射箭比赛.
(Ⅰ)通过抽签将他们安排到1~4号靶位,试求恰有两名运动员所抽靶位号与其参赛号码相同的概率;
(Ⅱ)记1号、2号射箭运动员射箭的环数为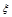 (
(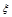 所有取值为0,1,2,3...,10)的概率分别为
所有取值为0,1,2,3...,10)的概率分别为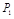 、
、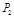 .根据教练员提供的资料,其概率分布如下表:
.根据教练员提供的资料,其概率分布如下表:
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
0 |
0 |
0 |
0 |
0.06 |
0.04 |
0.06 |
0.3 |
0.2 |
0.3 |
0.04 |
|
|
0 |
0 |
0 |
0 |
0.04 |
0.05 |
0.05 |
0.2 |
0.32 |
0.32 |
0.02 |
①1,2号运动员各射箭一次,求两人中至少有一人命中9环的概率;
②判断1号,2号射箭运动员谁射箭的水平高?并说明理由.
查看习题详情和答案>>