网址:http://m.1010jiajiao.com/timu_id_322026[举报]
如图所示,正方形单匝均匀线框abcd,边长L=0.4m,每边电阻相等,总电阻R=0.5Ω。一根足够长的绝缘轻质细线跨过两个轻质光滑定滑轮,一端连接正方形线框,另一端连接绝缘物体P。物体P放在一个光滑的足够长的固定斜面上,斜面倾角θ=30º,斜面上方的细线与斜面平行。在正方形线框正下方有一有界的匀强磁场,上边界Ⅰ和下边界Ⅱ都水平,两边界之间距离也是L=0.4m。磁场方向水平,垂直纸面向里,磁感应强度大小B=0.5T。现让正方形线框的cd边距上边界Ⅰ的正上方高度h=0.9m的位置由静止释放,且线框在运动过程中始终与磁场垂直,cd边始终保持水平,物体P始终在斜面上运动,线框刚好能以v=3m/s的速度进入匀强磁场并匀速通过匀强磁场区域。释放前细线绷紧,重力加速度g=10m/s2,不计空气阻力。
(1) 线框的cd边在匀强磁场中运动的过程中,c、d间的电压是多大?
(2) 线框的质量m1和物体P的质量m2分别是多大?
(3) 在cd边刚进入磁场时,给线框施加一个竖直向下的拉力F,使线框以进入磁场前的加速度匀加速通过磁场区域,在此过程中,力F做功W=0.23J,求正方形线框cd边产生的焦耳热是多少?

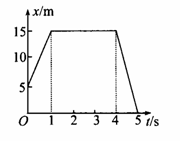
如下图所示是做直线运动的物体M在0~5 s的x-t图象,求:
(1)前3 s的平均速度 m/s (2分)
(2)全程的平均速度 m/s (2分)
(3)最后1 s的速度 m/s (2分)
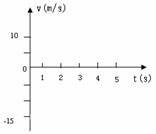
(4)请在右下图中画出该物体运动的V-t图象。(3分)
查看习题详情和答案>>
第一问 车和物体收到的力都是摩擦力
f=μmg 车的加速度a1=f/M=μmg/M=1m/s^2
滑块的加速度a2=f/m=μmg/m=5m/s^2
第二问 S=2.7m
假设不能从车上滑出 那么滑块最后必定停留在车上 并且和车具有同样的末速度 设为v'
因为系统在水平方向上所受的合外力为零 所以满足动量守恒
Mv+mv0=(M+m)*v' → v'=v0*m/(M+m)=7.5*10/(10+50)=1.25m/s
然后我们看能量 如果系统的初动能减去末动能 小于摩擦力所能做的最大功(就是滑块滑到头 但没掉下来) 那么假设成立 反之 不成立 不能明白的话 我们看下面具体的解答
先求系统的末动能 Ek'=1/2(M+m)v'^2=1/2*(50+10)*1.25^2=46.875(J)
系统的初动能 Ek=1/2mv0^2=1/2*10*7.5^2=281.25(J)
摩擦力所能做的最大功 W=fs=μmgs=0.5*10*10*3=150(J)
Ek-Ek'>W 所以也就是说 系统的初动能被摩擦力消耗掉一部分后【克服摩擦力做功】 所剩下的动能 还是要大于他们最后一起以同样的速度运动时的动能 因此滑块最后不肯能停在车上
那么 我们就来求滑块落地时与平板车右端间的水平距离
因为滑块滑出小车后 在水平方向上和小车都是做匀速运动
所以他们之间的距离 就是他们的速度差乘以滑块落地所需的时间
那么 我们就需要算出滑块的末速度v'和小车的末速度v''
现在有两个未知数 那就必须有两个方程
第一个方程是能量方程 Ek-W=1/2mv'^2+1/2Mv''^2
第二个方程是动量方程 mv0=mv'+Mv''
联立这两个方程 解得 v''=0.5m/s 或 v''=2m/s(舍掉)
从而得到v'=5m/s
接下来算滑块落地要多长时间
由h=1/2gt^2 带入数据 得t=0.6s
所以最后的答案: S=(v'-v'')*t=4.5*0.6=2.7m
查看习题详情和答案>>A.电池组,电动势6V
B.电流表,量程为500mA,内阻约为1Ω
C.电压表,量程为3V,内阻约为3kΩ
D.待测金属丝,电阻约为4Ω
E.螺旋测微器
F.米尺,最小刻度为1mm
G.滑动变阻器,最大阻值5Ω,最大电流2A
H.开关和导线若干
(1)在实验中,既要保证器材安全,又要减小误差,应选用的实验电路为

(2)该同学用螺旋测微器测量金属丝的直径,示数如下图所示.金属丝的直径d=

(3)测得金属丝长度L=51.00cm,电阻R=4.08Ω.则用d、L、R表示该金属丝的电阻率ρ=
| πRd2 |
| 4L |
| πRd2 |
| 4L |
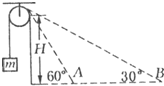 如图所示,一人通过大小不计的光滑定滑轮用细线拉一质量为m的物体,开始时手拉的绳头在滑轮正下方H处,当保持这一高度向右走,人的速度恒为v.试求在从A点走到B点的过程中:
如图所示,一人通过大小不计的光滑定滑轮用细线拉一质量为m的物体,开始时手拉的绳头在滑轮正下方H处,当保持这一高度向右走,人的速度恒为v.试求在从A点走到B点的过程中: