摘要: 已知动圆过定点.且与定直线相切. (1)求动圆圆心的轨迹C的方程, (2)若.是轨迹C上的两不同动点.且. 分别以.为切点作轨迹C的切线.设其交点Q.证明为定值. 21已知函数..为正的常数. (1)求函数的定义域, (2)求的单调区间.并指明单调性, (3)若..证明:. 安徽省两地三校2010届高三元旦联考数学(理)试卷
网址:http://m.1010jiajiao.com/timu_id_3209421[举报]
 .(本小题共13分)已知动圆过定点
.(本小题共13分)已知动圆过定点![]() ,且与直线
,且与直线![]() 相切.(1) 求动圆的圆心轨迹
相切.(1) 求动圆的圆心轨迹![]() 的方程;(2) 是否存在直线
的方程;(2) 是否存在直线![]() ,使
,使![]() 过点(0,1),并与轨迹
过点(0,1),并与轨迹![]() 交于
交于![]() 两点,且满足
两点,且满足![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
(本小题满分13分)
已知椭圆 :
:
 上的一动点
上的一动点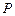 到右焦点的最短距离为
到右焦点的最短距离为 ,且右焦点到右准线的距离等于短半轴的长.
,且右焦点到右准线的距离等于短半轴的长.
(Ⅰ) 求椭圆 的方程;
的方程;
(Ⅱ) 过点 (
( ,
, )的动直线
)的动直线 交椭圆
交椭圆 于
于 、
、 两点,试问:在坐标平面上是否存在一个定点
两点,试问:在坐标平面上是否存在一个定点 ,使得无论
,使得无论 如何转动,以
如何转动,以
 为直径的圆恒过定点
为直径的圆恒过定点 ?若存在,求出点
?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(本小题满分13分)已知椭圆 的离心率为
的离心率为 ,以原点为圆心,椭圆短半轴长为半径的圆与直线
,以原点为圆心,椭圆短半轴长为半径的圆与直线 相切,
相切,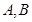 分别是椭圆的左右两个顶点,
分别是椭圆的左右两个顶点,  为椭圆
为椭圆 上的动点.
上的动点.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)若 与
与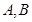 均不重合,设直线
均不重合,设直线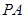 与
与 的斜率分别为
的斜率分别为 ,证明:
,证明: 为定值;
为定值;
(Ⅲ)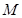 为过
为过 且垂直于
且垂直于 轴的直线上的点,若
轴的直线上的点,若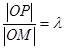 ,求点
,求点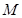 的轨迹方程,并说明轨迹是什么曲线.
的轨迹方程,并说明轨迹是什么曲线.
查看习题详情和答案>>
 ,定点A(2,0),M为圆C上一动点,点P在AM上,点N在C、M上(C为圆心),且满足
,定点A(2,0),M为圆C上一动点,点P在AM上,点N在C、M上(C为圆心),且满足 ,设点N的轨迹为曲线E.
,设点N的轨迹为曲线E. 的直线
的直线 交曲线E于C、D两点.若点Q(1,0)恰在以线段CD为直径的圆的内部,求实数m的取值范围.
交曲线E于C、D两点.若点Q(1,0)恰在以线段CD为直径的圆的内部,求实数m的取值范围. ,且其中一个焦点与抛物线
,且其中一个焦点与抛物线 的焦点重合.(Ⅰ)求椭圆C的方程;(Ⅱ)过点
的焦点重合.(Ⅰ)求椭圆C的方程;(Ⅱ)过点 的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过点T,若存在,求出点T的坐标;若不存在,请说明理由.
的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过点T,若存在,求出点T的坐标;若不存在,请说明理由.