摘要:21. 在数列 (I)求证:数列为等差数列, (II)若m为正整数.当
网址:http://m.1010jiajiao.com/timu_id_3207508[举报]
(本小题满分13分)
已知数列![]() 满足:
满足:![]() ,
,
![]()
(I)求![]() 得值;
得值;
(II)设![]() 求证:数列
求证:数列![]() 是等比数列,并求出其通项公式;
是等比数列,并求出其通项公式;
(III)对任意的![]() ,在数列
,在数列![]() 中是否存在连续的
中是否存在连续的![]() 项构成等差数列?若存在,写出这
项构成等差数列?若存在,写出这![]() 项,并证
项,并证![]() 明这
明这![]() 项构成等差数列;若不存在,说明理由.
项构成等差数列;若不存在,说明理由.
(本小题满分13分)已知函数f (x)=2n![]() 在[0,+
在[0,+![]() 上最小值是a
上最小值是a![]() (n∈N*).
(n∈N*).
(1)求数列{a![]() }的通项公式;(2)已知数列{b
}的通项公式;(2)已知数列{b![]() }中,对任意n∈N*都有b
}中,对任意n∈N*都有b![]() a
a![]() =1成立,设S
=1成立,设S![]() 为数列{b
为数列{b![]() }的前n项和,证明:2S
}的前n项和,证明:2S![]() <1;(3)在点列A
<1;(3)在点列A![]() (2n,a
(2n,a![]() )中是否存在两点A
)中是否存在两点A![]() ,A
,A![]() (i,j∈N*),使直线A
(i,j∈N*),使直线A![]() A
A![]() 的斜率为1?若存在,求出所有的数对(i,j);若不存在,请说明理由.
的斜率为1?若存在,求出所有的数对(i,j);若不存在,请说明理由.
 满足:
满足: ,
,

 得值;
得值; 求证:数列
求证:数列 是等比数列,并求出其通项公式;
是等比数列,并求出其通项公式; ,在数列
,在数列 项构成等差数列?若存在,写出这
项构成等差数列?若存在,写出这 明这
明这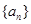 满足:
满足: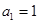 ,
,

 得值;
得值; 求证:数列
求证:数列 是等比数列,并求出其通项公式;
是等比数列,并求出其通项公式; ,在数列
,在数列 项构成等差数列?若存在,写出这
项构成等差数列?若存在,写出这