摘要：在如图7-26所示的三棱锥P-ABC中.PA⊥平面ABC.PA=AC=1.PC=BC.PB和平面ABC所成的角为30°. (1)求证:平面PBC⊥平面PAC, (2)比较三个侧面的面积的算术平均数与底面积数值的大小, (3)求AB的中点M到直线PC的距离.
网址：http://m.1010jiajiao.com/timu_id_3206584[举报]
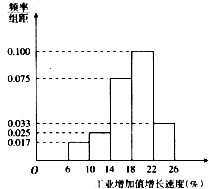（2011•北京模拟）经统计，2011年3月份30个地区工业增加值速度（%）．全部介于6与26之间，现将统计结果以4为组距分成5组：[6，10]，（10，14]，（14，18]，（18，22]，（22，26]，得到如图所示的频率分布直方图，那么工业增加值增长速度（%）在（10，18]的地区有（ ）
查看习题详情和答案>>
“世界睡眠日”定在每年的3月21日，2009年的世界睡眠日主题是“科学管理睡眠”，以提高公众对健康睡眠的自我管理能力和科学认识，为此某网站进行了持续一周的在线调查，共有200人参加调查，现将数据整理分组如题中表格所示．
（1）在答题卡给定的坐标系中画出频率分布直方图；
（2）睡眠时间小于8的概率是多少？
（3）为了对数据进行分析，采用了计算机辅助计算．分析中一部分计算见算法流程图（如图2），求输出的S的值，并说明S的统计意义．
查看习题详情和答案>>
| 序号（i） | 分组睡眠时间 | 组中值（mi） | 频数 （人数） |
频率 （fi） |
| 1 | [4，5） | 4.5 | 8 | 0.04 |
| 2 | [5，6） | 5.5 | 52 | 0.26 |
| 3 | [6，7） | 6.5 | 60 | 0.30 |
| 4 | [7，8） | 7.5 | 56 | 0.28 |
| 5 | [8，9） | 8.5 | 20 | 0.10 |
| 6 | [9，10] | 9.5 | 4 | 0.02 |
（1）在答题卡给定的坐标系中画出频率分布直方图；
（2）睡眠时间小于8的概率是多少？
（3）为了对数据进行分析，采用了计算机辅助计算．分析中一部分计算见算法流程图（如图2），求输出的S的值，并说明S的统计意义．
经统计，2011年3月份30个地区工业增加值速度（%）．全部介于6与26之间，现将统计结果以4为组距分成5组：[6，10]，（10，14]，（14，18]，（18，22]，（22，
26]，得到如图所示的频率分布直方图，那么工业增加值增长速度（%）在（10，18]的地区有（ ）
A．3个
B．7个
C．9个
D．12个
查看习题详情和答案>>
26]，得到如图所示的频率分布直方图，那么工业增加值增长速度（%）在（10，18]的地区有（ ）
A．3个
B．7个
C．9个
D．12个
查看习题详情和答案>>
（本小题共14分）国家教育部、体育总局和共青团中央曾共同号召，在全国各级各类学校要广泛、深入地开展全国亿万大中小学生阳光体育运动.为此某网站于2010年1月18日至24日，在全国范围内进行了持续一周的在线调查，随机抽取其中200名大中小学生的调查情况，就每天的睡眠时间分组整理如下表所示：
（1）估计每天睡眠时间小于8小时的学生所占的百分比约是多少；
（2）该网站利用如图所示的算法流程图，对样本数据作进一步统计分析，求输出的
的值，并说明的统计意义.
| 序号( | 每天睡眠时间 （小时） | 组中值( | 频数 | 频率 ( |
| 1 | [4，5) | 4.5 | 8 | 0.04 |
| 2 | [5，6) | 5.5 | 52 | 0.26 |
| 3 | [6，7) | 6.5 | 60 | 0.30 |
| 4 | [7，8) | 7.5 | 56 | 0.28 |
| 5 | [8，9) | 8.5 | 20 | 0.10 |
| 6 | [9，10) | 9.5 | 4 | 0.02 |
)
)
)
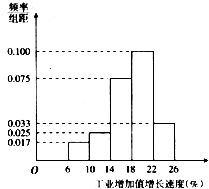经统计，2011年3月份30个地区工业增加值速度（%）．全部介于6与26之间，现将统计结果以4为组距分成5组：[6，10]，（10，14]，（14，18]，（18，22]，（22，