摘要：2．两点间的距离公式.不论A(x1.y1).B(x2.y2)在坐标平面上什么位置.都有d=|AB|=.特别地.与坐标轴平行的线段的长|AB|=|x2-x1|或|AB|=|y2-y1|.
网址：http://m.1010jiajiao.com/timu_id_3203298[举报]
下列语句表达不是算法的是
[ ]
A．
利用平面内两点间的距离公式求平面内M(0，0)与N(2，2)两点间的距离
B．
从长沙到北京的火车票是300元
C．
利用公式法解方程2x2＋x－1＝0
D．
利用公式S＝πr2，计算半径为3的圆的面积
下列语句表达不是算法的是
- A.利用平面内两点间的距离公式求平面内M(0，0)与N(2，2)两点间的距离
- B.从长沙到北京的火车票是300元
- C.利用公式法解方程2x2+x-1＝0
- D.利用公式S＝πr2，计算半径为3的圆的面积
在等差数列{an}中，a4S4=-14，S5-a5=-14，其中Sn是数列{an}的前n项之和，曲线Cn的方程是
+
=1，直线l的方程是y=x+3．
（1）求数列{an}的通项公式；
（2）判断Cn与l的位置关系；
（3）当直线l与曲线Cn相交于不同的两点An，Bn时，令Mn=（|an|+4）|AnBn|，求Mn的最小值．
（4）对于直线l和直线外的一点P，用“l上的点与点P距离的最小值”定义点P到直线l的距离与原有的点到直线距离的概念是等价的．若曲线Cn与直线l不相交，试以类似的方式给出一条曲线Cn与直线l间“距离”的定义，并依照给出的定义，在Cn中自行选定一个椭圆，求出该椭圆与直线l的“距离”．
查看习题详情和答案>>
| x2 |
| |an| |
| y2 |
| 4 |
（1）求数列{an}的通项公式；
（2）判断Cn与l的位置关系；
（3）当直线l与曲线Cn相交于不同的两点An，Bn时，令Mn=（|an|+4）|AnBn|，求Mn的最小值．
（4）对于直线l和直线外的一点P，用“l上的点与点P距离的最小值”定义点P到直线l的距离与原有的点到直线距离的概念是等价的．若曲线Cn与直线l不相交，试以类似的方式给出一条曲线Cn与直线l间“距离”的定义，并依照给出的定义，在Cn中自行选定一个椭圆，求出该椭圆与直线l的“距离”．
在等差数列
中，
，
，其中
是数列的前
项之和，曲线
的方程是
，直线
的方程是
．
求数列的通项公式；
当直线与曲线相交于不同的两点
，
时，令
，
求
的最小值；
对于直线和直线外的一点P，用“上的点与点P距离的最小值”定义点P到直线的距离与原有的点到直线距离的概念是等价的，若曲线与直线不相交，试以类似的方式给出一条曲线与直线间“距离”的定义，并依照给出的定义，在中自行选定一个椭圆，求出该椭圆与直线的“距离”．
在等差数列{an}中，a4S4=-14，S5-a5=-14，其中Sn是数列{an}的前n项之和，曲线Cn的方程是
+
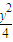=1，直线l的方程是y=x+3．
（1）求数列{an}的通项公式；
（2）判断Cn与l的位置关系；
（3）当直线l与曲线Cn相交于不同的两点An，Bn时，令Mn=（|an|+4）|AnBn|，求Mn的最小值．
（4）对于直线l和直线外的一点P，用“l上的点与点P距离的最小值”定义点P到直线l的距离与原有的点到直线距离的概念是等价的．若曲线Cn与直线l不相交，试以类似的方式给出一条曲线Cn与直线l间“距离”的定义，并依照给出的定义，在Cn中自行选定一个椭圆，求出该椭圆与直线l的“距离”．
查看习题详情和答案>>
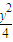+=1，直线l的方程是y=x+3．（1）求数列{an}的通项公式；
（2）判断Cn与l的位置关系；
（3）当直线l与曲线Cn相交于不同的两点An，Bn时，令Mn=（|an|+4）|AnBn|，求Mn的最小值．
（4）对于直线l和直线外的一点P，用“l上的点与点P距离的最小值”定义点P到直线l的距离与原有的点到直线距离的概念是等价的．若曲线Cn与直线l不相交，试以类似的方式给出一条曲线Cn与直线l间“距离”的定义，并依照给出的定义，在Cn中自行选定一个椭圆，求出该椭圆与直线l的“距离”．
查看习题详情和答案>>