摘要:21.⑴依题意.时...两式相减得
网址:http://m.1010jiajiao.com/timu_id_316114[举报]
已知数列{an}的通项为an=(2n-1)•2n,求其前n项和Sn时,我们用错位相减法,即
由Sn=1•2+3•22+5•23+…+(2n-1)•2n得2Sn=1•22+3•23+5•24+…+(2n-1)•2n+1
两式相减得-Sn=2+2•22+2•23+…+2•2n-(2n-1)•2n+1,
求出Sn=2-(2-2n)•2n+1.类比推广以上方法,若数列{bn}的通项为bn=n2•2n,则其前n项和Tn=
查看习题详情和答案>>
由Sn=1•2+3•22+5•23+…+(2n-1)•2n得2Sn=1•22+3•23+5•24+…+(2n-1)•2n+1
两式相减得-Sn=2+2•22+2•23+…+2•2n-(2n-1)•2n+1,
求出Sn=2-(2-2n)•2n+1.类比推广以上方法,若数列{bn}的通项为bn=n2•2n,则其前n项和Tn=
(n2-2n+3)•2n+1-6
(n2-2n+3)•2n+1-6
.数列 首项
首项 ,前
,前 项和
项和 满足等式
满足等式 (常数
(常数 ,
, ……)
……)
(1)求证: 为等比数列;
为等比数列;
(2)设数列 的公比为
的公比为 ,作数列
,作数列 使
使 (
( ……),求数列
……),求数列 的通项公式.
的通项公式.
(3)设 ,求数列
,求数列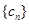 的前
的前 项和
项和 .
.
【解析】第一问利用由 得
得
两式相减得
故 时,
时,
从而 又
又 即
即 ,而
,而
从而 故
故
第二问中,
 又
又 故
故 为等比数列,通项公式为
为等比数列,通项公式为
第三问中,
 两边同乘以
两边同乘以
利用错位相减法得到和。
(1)由 得
得
两式相减得
故 时,
时,
从而 ………………3分
………………3分
又 即
即 ,而
,而
从而 故
故
 对任意
对任意 ,
, 为常数,即
为常数,即 为等比数列………………5分
为等比数列………………5分
(2)
 ……………………7分
……………………7分
又 故
故 为等比数列,通项公式为
为等比数列,通项公式为 ………………9分
………………9分
(3)
 两边同乘以
两边同乘以
 ………………11分
………………11分
两式相减得

查看习题详情和答案>>
已知数列{an}的通项为an=(2n-1)•2n,求其前n项和Sn时,我们用错位相减法,即
由Sn=1•2+3•22+5•23+…+(2n-1)•2n得2Sn=1•22+3•23+5•24+…+(2n-1)•2n+1
两式相减得-Sn=2+2•22+2•23+…+2•2n-(2n-1)•2n+1,
求出Sn=2-(2-2n)•2n+1.类比推广以上方法,若数列{bn}的通项为bn=n2•2n,则其前n项和Tn= . 查看习题详情和答案>>
由Sn=1•2+3•22+5•23+…+(2n-1)•2n得2Sn=1•22+3•23+5•24+…+(2n-1)•2n+1
两式相减得-Sn=2+2•22+2•23+…+2•2n-(2n-1)•2n+1,
求出Sn=2-(2-2n)•2n+1.类比推广以上方法,若数列{bn}的通项为bn=n2•2n,则其前n项和Tn= . 查看习题详情和答案>>