摘要:⑵求数列()最小的项. 文科数学评分参考
网址:http://m.1010jiajiao.com/timu_id_316082[举报]
已知二次函数f(x)=x2-2(10-3n)x+9n2-61n+100(n∈N*).
(1)设函数y=f(x)的图象的顶点的横坐标构成数列{an},求证:数列{an}是等差数列;
(2)在(1)的条件下,若数列{cn}满足cn=1+
(n∈N*),求数列{cn}中最大的项和最小的项.
查看习题详情和答案>>
(1)设函数y=f(x)的图象的顶点的横坐标构成数列{an},求证:数列{an}是等差数列;
(2)在(1)的条件下,若数列{cn}满足cn=1+
| 1 | ||
4n-
|
已知二次函数f(x)=x2-2(10-3n)x+9n2-61n+100(n∈N*).
(1)设函数y=f(x)的图象的顶点的横坐标构成数列{an},求证:数列{an}是等差数列;
(2)在(1)的条件下,若数列{cn}满足cn=1+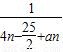 (n∈N*),求数列{cn}中最大的项和最小的项.
(n∈N*),求数列{cn}中最大的项和最小的项.
查看习题详情和答案>>
(1)设函数y=f(x)的图象的顶点的横坐标构成数列{an},求证:数列{an}是等差数列;
(2)在(1)的条件下,若数列{cn}满足cn=1+
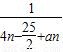 (n∈N*),求数列{cn}中最大的项和最小的项.
(n∈N*),求数列{cn}中最大的项和最小的项.查看习题详情和答案>>
a11,a12,…a18
a21,a22,…a28
…
a81,a82,…a88
64个正数排成8行8列,如上所示:在符合aij(1≤i≤8,1≤j≤8)中,i表示该数所在的行数,j表示该数所在的列数.已知每一行中的数依次都成等差数列,而每一列中的数依次都成等比数列(每列公比q都相等)且a11=
,a24=1,a32=
.
(1)若a21=
,求a12和a13的值.
(2)记第n行各项之和为An(1≤n≤8),数列{an}、{bn}、{cn}满足an=
,联mbn+1=2(an+mbn)(m为非零常数),cn=
,且c12+c72=100,求c1+c2+…c7的取值范围.
(3)对(2)中的an,记dn=
(n∈N),设Bn=d1•d2…dn(n∈N),求数列{Bn}中最大项的项数.
查看习题详情和答案>>
a21,a22,…a28
…
a81,a82,…a88
64个正数排成8行8列,如上所示:在符合aij(1≤i≤8,1≤j≤8)中,i表示该数所在的行数,j表示该数所在的列数.已知每一行中的数依次都成等差数列,而每一列中的数依次都成等比数列(每列公比q都相等)且a11=
| 1 |
| 2 |
| 1 |
| 4 |
(1)若a21=
| 1 |
| 4 |
(2)记第n行各项之和为An(1≤n≤8),数列{an}、{bn}、{cn}满足an=
| 36 |
| An |
| bn |
| an |
(3)对(2)中的an,记dn=
| 200 |
| an |
(2013•汕头二模)64个正数排成8行8列,如下所示: ,其中aij表示第i行第j列的数.已知每一行中的数依次都成等差数列,每一列中的数依次都成等比数列,且公比均为q,a11=
,其中aij表示第i行第j列的数.已知每一行中的数依次都成等差数列,每一列中的数依次都成等比数列,且公比均为q,a11=
,a24=1,a21=
.
(Ⅰ)求a12和a13的值;
(Ⅱ)记第n行各项之和为An(1≤n≤8),数列{an},{bn},{cn}满足an=
,mbn+1=2(an+mbn)(m为非零常数),cn=
,且
+
=100,求c1+c2+…+c7的取值范围;
(Ⅲ)对(Ⅱ)中的an,记dn=
(n∈N*),设Bn=d1d2…dn(n∈N*),求数列{Bn}中最大项的项数.
查看习题详情和答案>>
 ,其中aij表示第i行第j列的数.已知每一行中的数依次都成等差数列,每一列中的数依次都成等比数列,且公比均为q,a11=
,其中aij表示第i行第j列的数.已知每一行中的数依次都成等差数列,每一列中的数依次都成等比数列,且公比均为q,a11=| 1 |
| 2 |
| 1 |
| 4 |
(Ⅰ)求a12和a13的值;
(Ⅱ)记第n行各项之和为An(1≤n≤8),数列{an},{bn},{cn}满足an=
| 36 |
| An |
| bn |
| an |
| c | 2 1 |
| c | 2 7 |
(Ⅲ)对(Ⅱ)中的an,记dn=
| 200 |
| an |