摘要:A. B. C. D.⒏随机调查某校50个学生在“六一 儿童节的午餐费.结果如下表:餐费(元)345人数102020这50个学生“六一 节午餐费的平均值和方差分别是
网址:http://m.1010jiajiao.com/timu_id_316045[举报]
某校数学组为了选修课的设置,在设置的所有科目中随机抽取了30门,用问卷调查的方式对两个班的学生进行了普查。经统计,每一门选修课受学生喜欢的人次数如茎叶图所示。
如果要在这30门选出4门确立为选修课,并使得其中恰好有3门选修课受学生的喜欢人次数在[50,100]的概率是( )
A. | B. | C. | D. |
某校数学组为了选修课的设置,在设置的所有科目中随机抽取了30门,用问卷调查的方式对两个班的学生进行了普查。经统计,每一门选修课受学生喜欢的人次数如茎叶图所示。

如果要在这30门选出4门确立为选修课,并使得其中恰好有3门选修课受学生的喜欢人次数在[50,100]的概率是( )

如果要在这30门选出4门确立为选修课,并使得其中恰好有3门选修课受学生的喜欢人次数在[50,100]的概率是( )
A.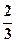 | B.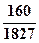 | C. | D.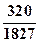 |
某中学研究性学习小组,为了考察高中学生的作文水平与爱看课外书的关系,在本校高三年级随机调查了50名学生.调査结果表明:在爱看课外书的25人中有18人作文水平好,另7人作文水平一般;在不爱看课外书的25人中有6人作文水平好,另19人作文水平一般.
(Ⅰ)试根据以上数据建立一个2×2列联表,并运用独立性检验思想,指出有多大把握认为中学生的作文水平与爱看课外书有关系?
(Ⅱ)将其中某5名爱看课外书且作文水平好的学生分别编号为1,2,3,4,5,某5名爱看课外书且作文水平一般的学生也分别编号为1,2,3,4,5,从这两组学生中各任选1人进行学习交流,求被选取的两名学生的编号之和为3的倍数或4的倍数的概率.
附:K2=
临界值表:
查看习题详情和答案>>
(Ⅰ)试根据以上数据建立一个2×2列联表,并运用独立性检验思想,指出有多大把握认为中学生的作文水平与爱看课外书有关系?
(Ⅱ)将其中某5名爱看课外书且作文水平好的学生分别编号为1,2,3,4,5,某5名爱看课外书且作文水平一般的学生也分别编号为1,2,3,4,5,从这两组学生中各任选1人进行学习交流,求被选取的两名学生的编号之和为3的倍数或4的倍数的概率.
附:K2=
| (a+b+c+d)(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
临界值表:
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
某中学研究性学习小组,为了考察高中学生的作文水平与爱看课外书的关系,在本校高三年级随机调查了50名学生.调査结果表明:在爱看课外书的25人中有18人作文水平好,另7人作文水平一般;在不爱看课外书的25人中有6人作文水平好,另19人作文水平一般.
(Ⅰ)试根据以上数据建立一个2×2列联表,并运用独立性检验思想,指出有多大把握认为中学生的作文水平与爱看课外书有关系?
(Ⅱ)将其中某5名爱看课外书且作文水平好的学生分别编号为1,2,3,4,5,某5名爱看课外书且作文水平一般的学生也分别编号为1,2,3,4,5,从这两组学生中各任选1人进行学习交流,求被选取的两名学生的编号之和为3的倍数或4的倍数的概率.
附:K2=
临界值表:
查看习题详情和答案>>
(Ⅰ)试根据以上数据建立一个2×2列联表,并运用独立性检验思想,指出有多大把握认为中学生的作文水平与爱看课外书有关系?
(Ⅱ)将其中某5名爱看课外书且作文水平好的学生分别编号为1,2,3,4,5,某5名爱看课外书且作文水平一般的学生也分别编号为1,2,3,4,5,从这两组学生中各任选1人进行学习交流,求被选取的两名学生的编号之和为3的倍数或4的倍数的概率.
附:K2=
| (a+b+c+d)(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
临界值表:
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |