摘要:由.又..∴在上是增函数.
网址:http://m.1010jiajiao.com/timu_id_314379[举报]
已知函数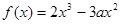 ,
, ,又函数
,又函数 在
在 单调递减,而在
单调递减,而在 单调递增.
单调递增.
(1)求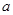 的值;
的值;
(2)求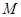 的最小值,使对
的最小值,使对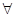
 ,有
,有 成立;
成立;
(3)是否存在正实数 ,使得
,使得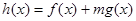 在
在 上既有最大值又有最小值?若存在,求出m的取值范围;若不存在,请说明理由.
上既有最大值又有最小值?若存在,求出m的取值范围;若不存在,请说明理由.
查看习题详情和答案>>
已知函数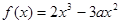 ,
,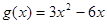 ,又函数
,又函数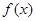 在
在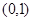 单调递减,而在
单调递减,而在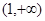 单调递增.
单调递增.
(1)求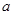 的值;
的值;
(2)求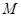 的最小值,使对
的最小值,使对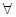
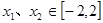 ,有
,有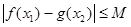 成立;
成立;
(3)是否存在正实数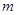 ,使得
,使得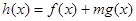 在
在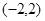 上既有最大值又有最小值?若存在,求出m的取值范围;若不存在,请说明理由.
上既有最大值又有最小值?若存在,求出m的取值范围;若不存在,请说明理由.
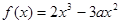 ,
,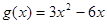 ,又函数
,又函数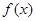 在
在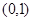 单调递减,而在
单调递减,而在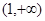 单调递增.
单调递增.(1)求
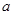 的值;
的值;(2)求
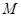 的最小值,使对
的最小值,使对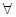
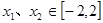 ,有
,有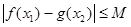 成立;
成立;(3)是否存在正实数
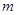 ,使得
,使得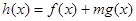 在
在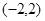 上既有最大值又有最小值?若存在,求出m的取值范围;若不存在,请说明理由.
上既有最大值又有最小值?若存在,求出m的取值范围;若不存在,请说明理由.已知函数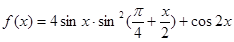 ,
,
(1)设常数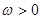 ,若
,若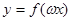 在区间
在区间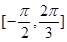 上是增函数,求
上是增函数,求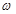 的取值范围;
的取值范围;
(2)设集合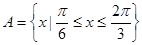 ,
,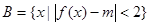 ,若
,若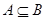 ,求
,求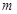 的取值范围.
的取值范围.
【解析】本试题主要考查了三角函数的性质的运用以及集合关系的运用。
第一问中利用
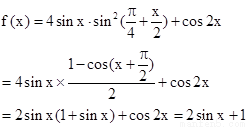
利用函数的单调性得到,参数的取值范围。
第二问中,由于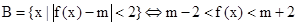 解得参数m的取值范围。
解得参数m的取值范围。
(1)由已知
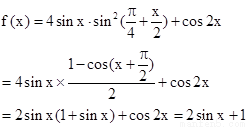
又因为常数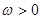 ,若
,若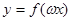 在区间
在区间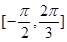 上是增函数故参数
上是增函数故参数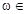

(2)因为集合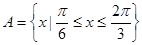 ,
,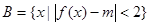 ,若
,若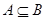
查看习题详情和答案>>