摘要：∴.显然直线过点
网址：http://m.1010jiajiao.com/timu_id_310221[举报]
有对称中心的曲线叫做有心曲线，显然圆、椭圆、双曲线都是有心曲线．过有心曲线的中心的弦叫有心曲线的直径（为研究方便，不妨设直径所在直线的斜率存在）．
定理：过圆x2+y2=r2（r＞0）上异于某直径两端点的任意一点，与这条直径的两个端点连线，则两条直线的斜率之积为定值-1．写出该定理在椭圆
+
=1(a＞b＞0)中的推广（不必证明）：
．
查看习题详情和答案>>
定理：过圆x2+y2=r2（r＞0）上异于某直径两端点的任意一点，与这条直径的两个端点连线，则两条直线的斜率之积为定值-1．写出该定理在椭圆
| x2 |
| a2 |
| y2 |
| b2 |
过椭圆
+
=1(a＞b＞0)上异于某直径两端点的任意一点，与这条直径的两个端点连线，则两条连线的斜率之积为定值-
| x2 |
| a2 |
| y2 |
| b2 |
| b2 |
| a2 |
过椭圆
+
=1(a＞b＞0)上异于某直径两端点的任意一点，与这条直径的两个端点连线，则两条连线的斜率之积为定值-
| x2 |
| a2 |
| y2 |
| b2 |
| b2 |
| a2 |
．
有对称中心的曲线叫做有心曲线，显然圆、椭圆、双曲线都是有心曲线．过有心曲线的中心的弦叫有心曲线的直径（为研究方便，不妨设直径所在直线的斜率存在）．
定理：过圆x2+y2=r2（r＞0）上异于某直径两端点的任意一点，与这条直径的两个端点连线，则两条直线的斜率之积为定值-1．写出该定理在椭圆
中的推广（不必证明）：
________
．
查看习题详情和答案>>
有对称中心的曲线叫做有心曲线，显然圆、椭圆、双曲线都是有心曲线．过有心曲线的中心的弦叫有心曲线的直径（为研究方便，不妨设直径所在直线的斜率存在）．
定理：过圆x2+y2=r2（r＞0）上异于某直径两端点的任意一点，与这条直径的两个端点连线，则两条直线的斜率之积为定值-1．写出该定理在椭圆
+
=1(a＞b＞0)中的推广（不必证明）：
______
．
查看习题详情和答案>>
定理：过圆x2+y2=r2（r＞0）上异于某直径两端点的任意一点，与这条直径的两个端点连线，则两条直线的斜率之积为定值-1．写出该定理在椭圆
| x2 |
| a2 |
| y2 |
| b2 |
______
．
中的推广（不必证明）：
＋
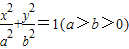＝1(a＞b＞0)中的推广(不必证明)________．