摘要:解得:t=6.5×10-9s
网址:http://m.1010jiajiao.com/timu_id_308836[举报]
(1)将0.
.化成分数,解题如下:
解:设S=0.
.记为①式
将①式两边都乘以10得 10S=3.
.记为②式
②-①得 10S-S=3.
.-0.
.即 9S=3
解得 S=
即0.
=
(2)按此方法化0.
,设S=0.
.
.
则
-0.
=
解得 S=
即0.
=
(3)请你按此方法把0.
0
化为分数.
查看习题详情和答案>>
| . |
| 3 |
解:设S=0.
| . |
| 3 |
将①式两边都乘以10得 10S=3.
| . |
| 3 |
②-①得 10S-S=3.
| . |
| 3 |
| . |
| 3 |
解得 S=
| 1 |
| 3 |
即0.
| . |
| 3 |
| 1 |
| 3 |
(2)按此方法化0.
| .. |
| 31 |
| .. |
| 31 |
100
100
S=31.| .. |
| 31 |
则
100
100
S-S=31.| .. |
| 31 |
| .. |
| 31 |
31
31
解得 S=
| 31 |
| 99 |
即0.
| .. |
| 31 |
| 31 |
| 99 |
| 31 |
| 99 |
(3)请你按此方法把0.
| . |
| 3 |
| . |
| 1 |
请阅读下列材料:
问题:现有5个边长为1的正方形,排列形式如图①,请把它们分割后拼接成一个新的正方形,要求:画出分割线并在正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形.
小东同学的做法是:设新正方形的边长为x(x>0),依题意,割补前后图形的面积相等,有x2=5,解得x=
,由此可知新正方形得边长等于两个小正方形组成得矩形对角线得长,于是,画出如图②所示的分割线,拼出如图③所示的新正方形.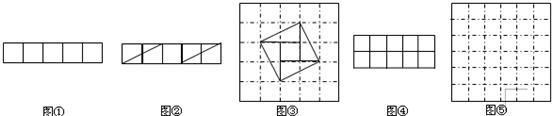
请你参考小东同学的做法,解决如下问题:
现有10个边长为1的正方形,排列形式如图④,请把它们分割后拼接成一个新的正方形,要求:在图④中画出分割线,并在图⑤的正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形.(说明:直接画出图形,不要求写分析过程.) 查看习题详情和答案>>
问题:现有5个边长为1的正方形,排列形式如图①,请把它们分割后拼接成一个新的正方形,要求:画出分割线并在正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形.
小东同学的做法是:设新正方形的边长为x(x>0),依题意,割补前后图形的面积相等,有x2=5,解得x=
| 5 |

请你参考小东同学的做法,解决如下问题:
现有10个边长为1的正方形,排列形式如图④,请把它们分割后拼接成一个新的正方形,要求:在图④中画出分割线,并在图⑤的正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形.(说明:直接画出图形,不要求写分析过程.) 查看习题详情和答案>>
甲、乙两库分别存原料290吨和190吨.若甲库每天调出50吨,乙库每天调人10吨,多少天后,乙库比甲库存的2倍还多10吨?解:设x天后,乙库比甲库存的2倍多10吨,依题意可列方程
.
查看习题详情和答案>>
2(290-50x)+10=190+10x
2(290-50x)+10=190+10x
,解得x=| 40 |
| 11 |
| 40 |
| 11 |
10、某厂把500万元资金投入新产品生产,一年后获得了一定的利润,在不抽掉资金和利润的前提下,第二年的利润率比第一年的利润率增加了8%,这样第二年净得利润112万元,为求第一年的利润率,可设它为x,则解得第一年的利润率是( )
查看习题详情和答案>>
如图(1),在Rt△ABC中,∠B=90°,AE平分∠BAC,将AB沿AE折叠,使点B落在AC上一点D处,已知AB=6,BC=8,可用下面的方法求线段BE的长:
由折叠可知:AD=AB=6,BE=DE,∠ADE=∠ABE=90°
在Rt△ABC中,∠B=90°,∴AC2=AB2+BC2=62+82=100
∴AC=10,CD=AC-AD=4,设BE=DE=x,则CE=8-x
在Rt△CED中,∠EDC=90°,∴EC2=ED2+CD2,即(8-x)2=x2+42,整理得:64-16x=16
解得:x=3
仿上面的解答法解答下题:
如图(2),在矩形ABCD中,AB=5cm,AD=13cm,在边CD上适当选定一点E,沿直线AE把△ADE折叠,使点D恰好落在边BC上一点F处,求DE的长度.

查看习题详情和答案>>
由折叠可知:AD=AB=6,BE=DE,∠ADE=∠ABE=90°
在Rt△ABC中,∠B=90°,∴AC2=AB2+BC2=62+82=100
∴AC=10,CD=AC-AD=4,设BE=DE=x,则CE=8-x
在Rt△CED中,∠EDC=90°,∴EC2=ED2+CD2,即(8-x)2=x2+42,整理得:64-16x=16
解得:x=3
仿上面的解答法解答下题:
如图(2),在矩形ABCD中,AB=5cm,AD=13cm,在边CD上适当选定一点E,沿直线AE把△ADE折叠,使点D恰好落在边BC上一点F处,求DE的长度.
