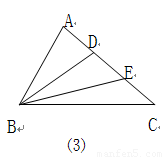
摘要：图3 图4 七.探究题:将一把三角尺放在边长为1的正方形ABCD上.并使它的直角顶点P在对角线AC上滑动.直角的一边始终经过点B.另一边与射线DC相交于点Q.设A.P两点间的距离为X.探究:(1)当点Q在边CD上时.线段PQ与线段PB之间有怎样的大小关系?试证明你得到的结论.(2)当点Q在边CD上时.设四边形PBCQ的面积为y.求y与x之间的函数解析式.并写出函数自变量的取值范围,(3)当点P在线段AC上滑动时.△PCQ是否可能成为等腰三角形?如果可能.指出所有能使△PCQ成为等腰三角形的点Q的位置.并求出响应的X的值,如果不可能.请说明理由. 答案
网址：http://m.1010jiajiao.com/timu_id_307[举报]
（本题满分12分）为了探究三角形的内切圆半径r与周长
、面积S之间的关系，在数学实验活动中，选取等边三角形(图甲)和直角三角形(图乙)进行研究.⊙O是△ABC的内切圆，切点分别为点D、E、F.
(1)用刻度尺分别量出表中未度量的△ABC的长，填入空格处，并计算出周长和面积S.(结果精确到0.1厘米)
|
|
AC |
BC |
AB |
r |
|
S |
|
图甲 |
|
|
|
0.6 |
|
|
|
图乙 |
|
|
|
1.0 |
|
|
(2)观察图形，利用上表实验数据分析.猜测特殊三角形的r与、S之间关系，并证明这种关系对任意三角形(图丙)是否也成立?
(3) 
查看习题详情和答案>>
（11分）
某同学从家里出发，骑自行车上学时，速度v（米/秒）与时间t（秒）的关系如图a，A（10，5），B（130，5），C（135，0）.
（1）求该同学骑自行车上学途中的速度v与时间t的函数关系式；
（2）计算该同学从家到学校的路程（提示：在OA和BC段的运动过程中的平均速度分别等于它们中点时刻的速度，路程＝平均速度×时间）；
（3）如图b，直线x＝t（0≤t≤135），与图a的图象相交于P、Q，用字母S表示图中阴影部分面积，试求S与t的函数关系式；
（4）由（2）（3），直接猜出在t时刻，该同学离开家所超过的路程与此时S的数量关系.
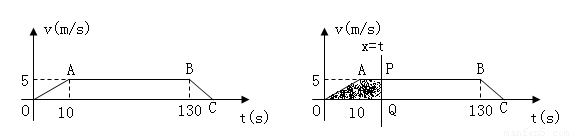
图a 图b
查看习题详情和答案>>
（本题满分12分）为了探究三角形的内切圆半径r与周长
、面积S之间的关系，在数学实验活动中，选取等边三角形(图甲)和直角三角形(图乙)进行研究.⊙O是△ABC的内切圆，切点分别为点D、E、F.
(1)用刻度尺分别量出表中未度量的△ABC的长，填入空格处，并计算出周长和面积S.(结果精确到0.1厘米)
(2)观察图形，利用上表实验数据分析.猜测特殊三角形的r与、S之间关系，并证明这种关系对任意三角形(图丙)是否也成立?
(3)
查看习题详情和答案>>
、面积S之间的关系，在数学实验活动中，选取等边三角形(图甲)和直角三角形(图乙)进行研究.⊙O是△ABC的内切圆，切点分别为点D、E、F.(1)用刻度尺分别量出表中未度量的△ABC的长，填入空格处，并计算出周长
和面积S.(结果精确到0.1厘米)| | AC | BC | AB | r | | S |
| 图甲 | | | | 0.6 | | |
| 图乙 | | | | 1.0 | | |
、S之间关系，并证明这种关系对任意三角形(图丙)是否也成立?(3)
查看习题详情和答案>>
层．将图1倒置后与原图1拼成图2的形状，这样我们可以算出图1中所有圆圈的个数为
．
，则最底层最左边这个圆圈中的数是 ；（2）我们自上往下，在每个圆圈中都按图4的方式填上一串连续的整数
，
，
，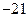