摘要:22.解:(Ⅰ)----1分
网址:http://m.1010jiajiao.com/timu_id_30440[举报]
(Ⅰ)解关于x的不等式:x2-2x+1-a2≥0;
(Ⅱ)已知集合A是函数y=lg(20+8x-x2)的定义域,p:x∈A,q:x2-2x+1-a2≥0(a>0),若?p是q的充分不必要条件,求a的取值范围.
查看习题详情和答案>>
(Ⅱ)已知集合A是函数y=lg(20+8x-x2)的定义域,p:x∈A,q:x2-2x+1-a2≥0(a>0),若?p是q的充分不必要条件,求a的取值范围.
(Ⅰ)阅读理解:
①对于任意正实数a,b,∵(
-
)2≥0, ∴a-2
+b≥0,∴a+b≥2
只有当a=b时,等号成立.
②结论:在a+b≥2
(a,b均为正实数)中,若ab为定值p,则a+b≥2
,
只有当a=b时,a+b有最小值2
.
(Ⅱ)结论运用:根据上述内容,回答下列问题:(提示:在答题卡上作答)
①若m>0,只有当m= 时,m+
有最小值 .
②若m>1,只有当m= 时,2m+
有最小值 .
(Ⅲ)探索应用:
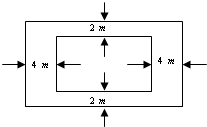
学校要建一个面积为392m2的长方形游泳池,并且在四周要修建出宽为2m和4m的小路(如图).问游泳池的长和宽分别为多少米时,共占地面积最小?并求出占地面积的最小值.
查看习题详情和答案>>
①对于任意正实数a,b,∵(
| a |
| b |
| ab |
| ab |
只有当a=b时,等号成立.
②结论:在a+b≥2
| ab |
| p |
只有当a=b时,a+b有最小值2
| p |
(Ⅱ)结论运用:根据上述内容,回答下列问题:(提示:在答题卡上作答)
①若m>0,只有当m=
| 1 |
| m |
②若m>1,只有当m=
| 8 |
| m-1 |
(Ⅲ)探索应用:
学校要建一个面积为392m2的长方形游泳池,并且在四周要修建出宽为2m和4m的小路(如图).问游泳池的长和宽分别为多少米时,共占地面积最小?并求出占地面积的最小值.

解:因为有负根,所以![]() 在y轴左侧有交点,因此
在y轴左侧有交点,因此![]()
解:因为函数没有零点,所以方程![]() 无根,则函数y=x+|x-c|与y=2没有交点,由图可知c>2
无根,则函数y=x+|x-c|与y=2没有交点,由图可知c>2
13.证明:(1)令x=y=1,由已知可得f(1)=f(1×1)=f(1)f(1),所以f(1)=1或f(1)=0
若f(1)=0,f(0)=f(1×0)=f(1)f(0)=0,所以f(1)=f(0)与已知条件“![]() ”矛盾所以f(1)≠0,因此f(1)=1,所以f(1)-1=0,1是函数y=f(x)-1的零点
”矛盾所以f(1)≠0,因此f(1)=1,所以f(1)-1=0,1是函数y=f(x)-1的零点
(2)因为f(1)=f[(-1)×(-1)]=f2(-1)=,所以f(-1)=±1,但若f(-1)=1,则f(-1)=f(1)与已知矛盾所以f(-1)不能等于1,只能等于-1。所以任x∈R,f(-x)=f(-1)f(x)=-f(x),因此函数是奇函数
数字1,2,3,4恰好排成一排,如果数字i(i=1,2,3,4)恰好出现在第i个位置上则称有一个巧合,求巧合数![]() 的分布列。
的分布列。