网址:http://m.1010jiajiao.com/timu_id_302857[举报]
一、选择题: B C A D B C A B D C
二、填空题:
11、 12、
12、 13、
13、
14、 15、②③
15、②③
三、解答题:
16.解:(1)  ……………………………1分
……………………………1分
 =
=
= =
= …………………………………………4分
…………………………………………4分
∵θ∈[π,2π],∴ ,
,
∴ ≤1 则
≤1 则  max=2
max=2 . ………………………………………………6分
. ………………………………………………6分
(2) 由已知 ,得
,得 …………………………………8分
…………………………………8分
又 ∴
∴ ……………………10分
……………………10分
∵θ∈[π,2π]∴ ,∴
,∴ . …………………12分
. …………………12分
17.解:依题意知: .……4分
.……4分
(1)对于
且 是奇函数……………………………………….……6分
是奇函数……………………………………….……6分
(2) 当
当 时,
时, 单调递减,
单调递减,
当 时,
时, 单调递增………………………………………….…8分
单调递增………………………………………….…8分
 ……….…………..…10分
……….…………..…10分
又 ………….……12分
………….……12分
18.解:(1)当
 ………………2分
………………2分

 ,..............................................5分
,..............................................5分
故 ................6分
................6分
定义域为 .................................7分
.................................7分
(2)对于 ,
,
显然当 (元), ..................................9分
(元), ..................................9分

∴当每辆自行车的日租金定在11元时,才能使一日的净收入最多。..........12分
19.解:(1)由题意
 …………………………2分
…………………………2分
 当
当 时,
时, 取得极值,
取得极值,  所以
所以 

 即
即  …………………4分
…………………4分
此时当 时,
时, ,当
,当 时,
时, ,
,
 是函数
是函数 的最小值。
………………………6分
的最小值。
………………………6分
(2)设 ,则
,则  ,
, ……8分
……8分
设 ,
,
 ,令
,令 解得
解得 或
或
列表如下:











__
0
+










 函数
函数 在
在 和
和 上是增函数,在
上是增函数,在 上是减函数。
上是减函数。
当 时,
时, 有极大值
有极大值 ;当
;当 时,
时, 有极小值
有极小值 ……10分
……10分
 函数
函数 与
与 的图象有两个公共点,
的图象有两个公共点, 函数
函数 与
与 的图象有两个公共点
的图象有两个公共点
 或
或 
 ……12分
……12分
20.解:(1)
 ,
,
 .令
.令 ,则
,则 .…………2分
.…………2分
 ,
, 当
当 时,
时, ,则
,则 .
. 数列
数列 不是等比数列.
不是等比数列.
 当
当 时,数列
时,数列 不是等比数列.………………… 5分
不是等比数列.………………… 5分
当 时,
时, ,则数列
,则数列 是等比数列,且公比为2.
是等比数列,且公比为2.
 ,即
,即 .解得
.解得 .……7分
.……7分
(2)由(Ⅰ)知,当 时,
时, ,
,
 .
.
令 , ………………………①
, ………………………①
则 , …………②
, …………②
由①-②:

 ,
,
 , ………………………………..………11分
, ………………………………..………11分
则
 . …………………..………13分
. …………………..………13分
21.解:(1)∵ 成等比数列 ∴
成等比数列 ∴
 设
设 是椭圆上任意一点,依椭圆的定义得
是椭圆上任意一点,依椭圆的定义得
即 为所求的椭圆方程.
……………………5分
为所求的椭圆方程.
……………………5分
(2)假设 存在,因
存在,因 与直线
与直线 相交,不可能垂直
相交,不可能垂直 轴 …………………6分
轴 …………………6分
因此可设 的方程为:
的方程为: 由
由

 ① ……………………8分
① ……………………8分
方程①有两个不等的实数根
∴ ② ………10分
② ………10分
设两个交点 、
、 的坐标分别为
的坐标分别为 ∴
∴
∵线段 恰被直线
恰被直线 平分 ∴
平分 ∴
∵ ∴
∴ ③ 把③代入②得
③ 把③代入②得 
∵ ∴
∴ ∴
∴ 解得
解得 或
或 ………13分
………13分
∴直线 的倾斜角范围为
的倾斜角范围为 …………………14分
…………………14分
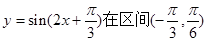 内单调递增
内单调递增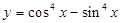 的最小正周期为2
的最小正周期为2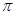
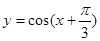 的图像是关于点
的图像是关于点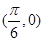 成中心对称的图形
成中心对称的图形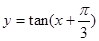 的图像是关于直线
的图像是关于直线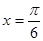 成轴对称的图形
成轴对称的图形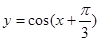 的图像是关于点
的图像是关于点 成中心对称的图形
成中心对称的图形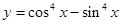 的最小正周期为2
的最小正周期为2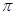
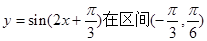 内单调递增
内单调递增 的图像是关于直线
的图像是关于直线 成轴对称的图形
成轴对称的图形 的图像是关于点
的图像是关于点 成中心对称的图形
成中心对称的图形 的最小正周期为2
的最小正周期为2
 内单调递增
内单调递增 的图像是关于直线
的图像是关于直线 成轴对称的图形
成轴对称的图形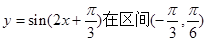 内单调递增
内单调递增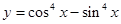 的最小正周期为2
的最小正周期为2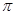
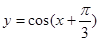 的图像是关于点
的图像是关于点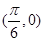 成中心对称的图形
成中心对称的图形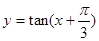 的图像是关于直线
的图像是关于直线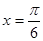 成轴对称的图形
成轴对称的图形