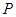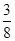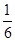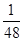摘要:由(1)知.恰有一件测试不合格的概率为
网址:http://m.1010jiajiao.com/timu_id_281868[举报]
学校要用三辆车从北湖校区把教师接到文庙校区,已知从北湖校区到文庙校区有两条公路,汽车走公路①堵车的概率为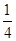 ,不堵车的概率为
,不堵车的概率为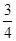 ;汽车走公路②堵车的概率为
;汽车走公路②堵车的概率为 ,不堵车的概率为
,不堵车的概率为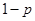 ,若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响。(I)若三辆车中恰有一辆车被堵的概率为
,若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响。(I)若三辆车中恰有一辆车被堵的概率为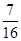 ,求走公路②堵车的概率;(Ⅱ)在(I)的条件下,求三辆车中被堵车辆的个数
,求走公路②堵车的概率;(Ⅱ)在(I)的条件下,求三辆车中被堵车辆的个数 的分布列和数学期望。
的分布列和数学期望。
【解析】第一问中,由已知条件结合n此独立重复试验的概率公式可知,得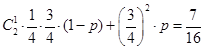
第二问中 可能的取值为0,1,2,3
可能的取值为0,1,2,3 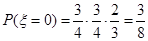 ,
, 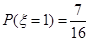
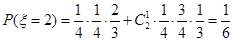 ,
,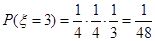
从而得到分布列和期望值
解:(I)由已知条件得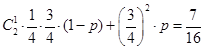 ,即
,即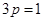 ,则
,则 的值为
的值为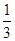 。
。
(Ⅱ) 可能的取值为0,1,2,3
可能的取值为0,1,2,3 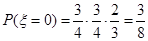 ,
, 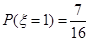
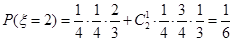 ,
,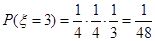
 的分布列为:(1分)
的分布列为:(1分)
|
|
0 |
1 |
2 |
3 |
|
|
|
|
|
|
所以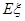
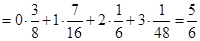
查看习题详情和答案>>
学校要用三辆车从北湖校区把教师接到文庙校区,已知从北湖校区到文庙校区有两条公路,汽车走公路①堵车的概率为
,不堵车的概率为
;汽车走公路②堵车的概率为p,不堵车的概率为1-p,若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响.
(I)若三辆车中恰有一辆车被堵的概率为
,求走公路②堵车的概率;
(Ⅱ)在(I)的条件下,求三辆车中被堵车辆的个数为2的概率.
查看习题详情和答案>>
| 1 |
| 4 |
| 3 |
| 4 |
(I)若三辆车中恰有一辆车被堵的概率为
| 7 |
| 16 |
(Ⅱ)在(I)的条件下,求三辆车中被堵车辆的个数为2的概率.
学校要用三辆校车从南校区把教职工接到校本部,已知从南校区到校本部有两条公路,校车走公路①堵车的概率为
,不堵车的概率为
;校车走公路②堵车的概率为,不堵车的概率为1-p.若甲、乙两辆校车走公路①,丙校车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响.
(Ⅰ)若三辆校车中恰有一辆校车被堵的概率为
,求走公路②堵车的概率;
(Ⅱ)在(I)的条件下,求三辆校车中被堵车辆的辆数ξ的分布列和数学期望.
查看习题详情和答案>>
| 1 |
| 4 |
| 3 |
| 4 |
(Ⅰ)若三辆校车中恰有一辆校车被堵的概率为
| 7 |
| 16 |
(Ⅱ)在(I)的条件下,求三辆校车中被堵车辆的辆数ξ的分布列和数学期望.