摘要：又通过知:.
网址：http://m.1010jiajiao.com/timu_id_262468[举报]
已知二次函数k≤1图象经过坐标原点，其导函数为f′（x）=6x-2，数列{an}的前n项和为Sn，点（n，Sn）（n∈N*）均在函数y=f（x）的图象上；又b1=1，cn=
（an+2），且1+2a2+22b3+…+2n-2bn-1+2n-1bn=cn，对任意n∈N*都成立，
（1）求数列{an}，{bn}的通项公式；
（2）求数列{cn•bn}的前n项和Tn；
（3）求证：（i）ln（x+1）＜（x＞0）；（ii）
＜
（n∈N*，n≥2）．
查看习题详情和答案>>
| 1 |
| 3 |
（1）求数列{an}，{bn}的通项公式；
（2）求数列{cn•bn}的前n项和Tn；
（3）求证：（i）ln（x+1）＜（x＞0）；（ii）
| n |
 |
| i=2 |
| lnai |
| ai2 |
| 2n2-n-1 |
| 4(n+1) |
已知二次函数k≤1图象经过坐标原点，其导函数为f′（x）=6x-2，数列{an}的前n项和为Sn，点（n，Sn）（n∈N*）均在函数y=f（x）的图象上；又b1=1，cn=
（an+2），且1+2a2+22b3+…+2n-2bn-1+2n-1bn=cn，对任意n∈N*都成立，
（1）求数列{an}，{bn}的通项公式；
（2）求数列{cn•bn}的前n项和Tn；
（3）求证：（i）ln（x+1）＜（x＞0）；（ii）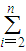
＜
（n∈N*，n≥2）．
查看习题详情和答案>>
（an+2），且1+2a2+22b3+…+2n-2bn-1+2n-1bn=cn，对任意n∈N*都成立，（1）求数列{an}，{bn}的通项公式；
（2）求数列{cn•bn}的前n项和Tn；
（3）求证：（i）ln（x+1）＜（x＞0）；（ii）
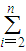
＜（n∈N*，n≥2）．查看习题详情和答案>>
| |||||||||||
N+)．
＋
的最小值．
＋
＝(
＋
)(x＋2y)＝3＋
＋
≥3＋2
．
＋
＝1，又x＋y的最小值为18，求a，b(a＞b)的值．