网址:http://m.1010jiajiao.com/timu_id_249125[举报]
一、选择题:(1)-(12)CAADB BAACD CA
二、填空题:(13).files/image092.gif) (14)
(14).files/image247.gif) (15)
(15).files/image249.gif) (16)
(16).files/image251.gif)
三、解答题:
(17)解:(1).files/image253.gif)
.files/image255.gif)
.files/image257.gif)
.files/image259.gif) …………6分
…………6分
(2).files/image261.gif) …………8分
…………8分
.files/image263.gif)
.files/image265.gif) 时,
时,.files/image267.gif)
当.files/image269.gif) 时,
时,.files/image271.gif)
当.files/image273.gif) 时,
时,.files/image275.gif) ……11分
……11分
综上所述:.files/image277.gif) ………………12分
………………12分
(18)解:(1)每家煤矿必须整改的概率1-0.5,且每家煤矿是否整改是相互独立的,所以恰好有两家煤矿必须整改的概率是
.files/image279.gif) ………………4分
………………4分
(2)由题设,必须整改的煤矿数.files/image281.gif) 服从二项分布
服从二项分布.files/image283.gif) ,从而
,从而.files/image281.gif) 的数学期望是
的数学期望是
.files/image285.gif) ,即平均有2.50家煤矿必须整改. ………………8分
,即平均有2.50家煤矿必须整改. ………………8分
(3)某煤矿被关闭,即煤矿第一次安检不合格,整改后复查仍不合格,所以该煤矿被关闭的概率是.files/image287.gif) ,从而该煤矿不被关闭的概率是0.9,由题意,每家煤矿是否关闭是相互独立的,所以5家煤矿都不被关闭的概率是
,从而该煤矿不被关闭的概率是0.9,由题意,每家煤矿是否关闭是相互独立的,所以5家煤矿都不被关闭的概率是
.files/image289.gif)
从而至少关闭一家煤矿的概率是.files/image291.gif) ………………12分
………………12分
(19)证明:由多面体.files/image293.gif) 的三视图知,四棱锥
的三视图知,四棱锥.files/image295.gif) 的底面
的底面.files/image297.gif) 是边长为
是边长为.files/image299.gif) 的正方形,侧面
的正方形,侧面.files/image301.gif) 是等腰三角形,
是等腰三角形,.files/image303.gif) ,
,
且平面.files/image305.gif) 平面
平面.files/image297.gif) .……2分
.……2分
(1)
.files/image307.gif) 连结
连结.files/image309.gif) ,则
,则.files/image311.gif) 是
是.files/image313.gif) 的中点,
的中点,
在△.files/image315.gif) 中,
中,.files/image317.gif) ,………4分
,………4分
且.files/image319.gif)
.files/image321.gif) 平面
平面.files/image301.gif) ,
,.files/image324.gif)
.files/image326.gif) 平面
平面.files/image301.gif) ,
,
∴.files/image324.gif) ∥平面
∥平面.files/image301.gif) ………6分
………6分
(2)
因为平面.files/image301.gif) ⊥平面
⊥平面.files/image297.gif) ,
,
平面.files/image301.gif) ∩平面
∩平面.files/image330.gif) ,
,
又.files/image332.gif) ⊥
⊥.files/image334.gif) ,所以,
,所以,.files/image332.gif) ⊥平面
⊥平面.files/image301.gif) ,
,
∴.files/image332.gif) ⊥
⊥.files/image319.gif) …………8分
…………8分
又.files/image303.gif) ,
,.files/image338.gif) ,所以△
,所以△.files/image301.gif) 是
是
等腰直角三角形,
且.files/image340.gif) ,即
,即.files/image342.gif) ………………10分
………………10分
又.files/image344.gif) , ∴
, ∴ .files/image346.gif) 平面
平面.files/image348.gif) ,
,
又.files/image319.gif)
.files/image321.gif) 平面
平面.files/image301.gif) ,
,
所以 平面.files/image301.gif) ⊥平面
⊥平面.files/image348.gif) ………………12分
………………12分
(20)解:设.files/image353.gif)
由.files/image355.gif)
.files/image357.gif)
.files/image359.gif)
即.files/image361.gif)
.files/image363.gif) ,
,
.files/image365.gif) ………………6分
………………6分
(2)由题意得.files/image367.gif) 上恒成立。
上恒成立。
即.files/image369.gif) 在[-1,1]上恒成立。
在[-1,1]上恒成立。
设.files/image371.gif) 其图象的对称轴为直线
其图象的对称轴为直线.files/image373.gif) ,所以
,所以.files/image375.gif) 上递减,
上递减,
故只需,.files/image377.gif) ,即
,即.files/image379.gif) ………………12分
………………12分
(21)解:(I)由.files/image381.gif)
.files/image383.gif)
.files/image385.gif)
.files/image387.gif)
.files/image389.gif)
所以,数列.files/image391.gif) …………6分
…………6分
(II)由.files/image393.gif) 得:
得:
.files/image395.gif)
.files/image397.gif)
.files/image399.gif) …………(1)
…………(1)
.files/image401.gif) …………(2) …………10分
…………(2) …………10分
(2)-(1)得:.files/image403.gif)
.files/image405.gif)
.files/image407.gif) …………12分
…………12分
(22)解:(Ⅰ)∵.files/image409.gif)
∵直线.files/image411.gif) 相切,
相切,
∴.files/image413.gif) ∴
∴.files/image415.gif) …………3分
…………3分
∵椭圆C1的方程是 .files/image417.gif) ………………6分
………………6分
(Ⅱ)∵MP=MF2,
∴动点M到定直线.files/image419.gif) 的距离等于它到定点F1(1,0)的距离,
的距离等于它到定点F1(1,0)的距离,
∴动点M的轨迹是C为l1准线,F2为焦点的抛物线 ………………6分
∴点M的轨迹C2的方程为 .files/image421.gif) …………9分
…………9分
(Ⅲ)Q(0,0),设.files/image423.gif)
∴.files/image425.gif)
∵.files/image427.gif)
∴.files/image429.gif)
∵.files/image431.gif) ,化简得
,化简得
∴.files/image433.gif) ………………11分
………………11分
∴.files/image435.gif)
当且仅当
.files/image437.gif) 时等号成立 …………13分
时等号成立 …………13分
∵.files/image439.gif)
∴当.files/image441.gif) 的取值范围是
的取值范围是.files/image443.gif)
……14分
已知椭圆![]() 的离心率为
的离心率为![]() 以原点O为圆心,椭圆的短半轴长为半径的圆与直线
以原点O为圆心,椭圆的短半轴长为半径的圆与直线![]() 相切。
相切。
(I)求椭圆C的方程;
(II)设P(4,0),A,B是椭圆C上关于x轴对称的任意两个不同的点,连结PB交椭圆C于另一点E,证明直线AE与x轴交于定点Q;
(III)在(II)条件下,过点Q的直线与椭圆C交于M,N两点,求![]() 的取值范围。
的取值范围。
已知椭圆![]() 的离心率为
的离心率为![]() 以原点O为圆心,椭圆的短半轴长为半径的圆与直线
以原点O为圆心,椭圆的短半轴长为半径的圆与直线![]() 相切。
相切。
(I)求椭圆C的方程;
(II)设P(4,0),A,B是椭圆C上关于x轴对称的任意两个不同的点,连结PB交椭圆C于另一点E,证明直线AE与x轴交于定点Q;
(III)在(II)条件下,过点Q的直线与椭圆C交于M,N两点,求![]() 的取值范围。
的取值范围。
 (a>b>0)的离心率为
(a>b>0)的离心率为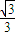 ,直线l:y=x+2与以原点为圆心,椭圆C1的短半轴长为半径的圆相切.
,直线l:y=x+2与以原点为圆心,椭圆C1的短半轴长为半径的圆相切.(I)求椭圆C1的方程;
(II)直线l1过椭圆C1的左焦点F1,且与x轴垂直,动直线l2垂直于直线l2,垂足为点P,线段PF2的垂直平分线交l2于点M,求点M的轨迹C2的方程;
(III)设C2上的两个不同点R、S满足
 ,求
,求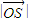 的取值范围(O为坐标原点).
的取值范围(O为坐标原点).查看习题详情和答案>>
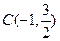 ,以A、B为焦点的椭圆经过点C。
,以A、B为焦点的椭圆经过点C。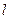 与椭圆交于不同两点M、N,使
与椭圆交于不同两点M、N,使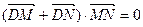 ?若存在,求出直线
?若存在,求出直线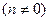 ,存在不平行于x轴的直线
,存在不平行于x轴的直线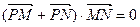 ,试求实数n的取值范围。
,试求实数n的取值范围。