摘要：整理得.即为曲线C的方程．
网址：http://m.1010jiajiao.com/timu_id_248761[举报]
已知曲线C:
(m∈R)
（1） 若曲线C是焦点在x轴点上的椭圆，求m的取值范围；
（2） 设m=4，曲线c与y轴的交点为A，B（点A位于点B的上方），直线y=kx+4与曲线c交于不同的两点M、N,直线y=1与直线BM交于点G.求证：A，G，N三点共线。
【解析】（1）曲线C是焦点在x轴上的椭圆，当且仅当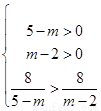
解得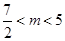
，所以m的取值范围是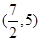
(2)当m=4时，曲线C的方程为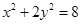
，点A,B的坐标分别为
，
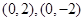由
，得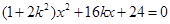
因为直线与曲线C交于不同的两点，所以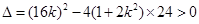
即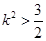
设点M，N的坐标分别为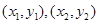
，则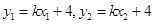
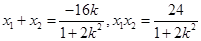
直线BM的方程为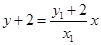
，点G的坐标为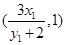
因为直线AN和直线AG的斜率分别为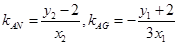
所以
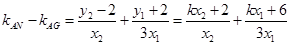
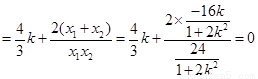
即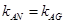
,故A，G，N三点共线。
查看习题详情和答案>>
已知直线l：
（t为参数），以坐标原点为极点，x轴正半轴为极轴，曲线C的极坐标方程为ρ=
cos(θ+
)．
（1）将曲线C的方程化成直角坐标方程；
（2）求直线l被曲线C截得的弦长．
查看习题详情和答案>>
|
| 2 |
| π |
| 4 |
（1）将曲线C的方程化成直角坐标方程；
（2）求直线l被曲线C截得的弦长．
已知点M（0，-1），直线l：y=mx+1与曲线C：ax2+y2=2（m，a∈R）交于A、B两点．
（1）当m=0时，有∠AOB=
，求曲线C的方程；
（2）当实数a为何值时，对任意m∈R，都有
•
为定值T？指出T的值；
（3）设动点P满足
=
+
，当a=-2，m变化时，求点P的轨迹方程；
（4）是否存在常数M，使得对于任意的a∈（0，1），m∈R，都有
•
＜M恒成立？如果存在，求出的M得最小值；如果不存在，说明理由．
查看习题详情和答案>>
（1）当m=0时，有∠AOB=
| π |
| 3 |
（2）当实数a为何值时，对任意m∈R，都有
| OA |
| OB |
（3）设动点P满足
| MP |
| OA |
| OB |
（4）是否存在常数M，使得对于任意的a∈（0，1），m∈R，都有
| OA |
| OB |