摘要：(1)已知三条公路.要在三条公路两两交叉的中间三角形部分修建一个尽可能大的圆形花坛.请你设计出示意图.(不写作法.保留作图痕迹)
网址：http://m.1010jiajiao.com/timu_id_24412[举报]
21、作图．
（1）已知△ABC，在△ABC内求作一点P，使点P到△ABC三条边的距离相等．
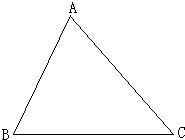
（2）要在高速公路旁边修建一个飞机场，使飞机场到A、B两个城市的距离之和最小，请做出飞机场的位置．
查看习题详情和答案>>
（1）已知△ABC，在△ABC内求作一点P，使点P到△ABC三条边的距离相等．
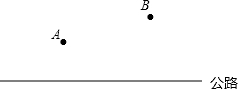
（2）要在高速公路旁边修建一个飞机场，使飞机场到A、B两个城市的距离之和最小，请做出飞机场的位置．
作图．
（1）已知△ABC，在△ABC内求作一点P，使点P到△ABC三条边的距离相等．
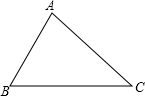
（2）要在高速公路旁边修建一个飞机场，使飞机场到A、B两个城市的距离之和最小，请作出飞机场的位置．
查看习题详情和答案>>
如图，已知：AB＝AD，D是BC中点，E是AD上任意一点，连接EB、EC，求证：EB＝EC．
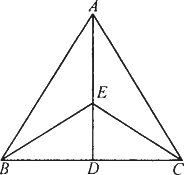
分析：(1)观察图形，图中线段EB和线段EC是________三角形中的边．现需证EB＝EC，可证△ABE≌________或△BED≌________．
(2)由已知可得BD＝CD，不要忽略图形中隐含的已知条件AE、DE、AD是三对全等三角形的公共边．
(3)找需知，只需证得∠BAE＝∠CAE或∠BDE＝∠CDE，即可得到上述两个三角形全等(恰当选择SAS来判定)．
(4)再看已知，三组对应边对应相等，可以利用SSS来证明△ABD≌△ACD，就得到∠BAE＝∠CAE或∠BDE＝∠CDE．
请同学们完成下列填空
证明一：∵D是BC中点 ∴BD＝CD
在△ABD和△ACD中，
________
________
________
∴△ABD≌△ACD(SSS)
∴∠BAE＝∠CAE(全等三角形的对应角相等)
在△ABE和△ACE中，
________
________
________
∴△ABE≌△ACE(SAS)
∴EB＝EC(全等三角形的对应边相等)
(请同学们根据分析思路，写出第二种证明方法)
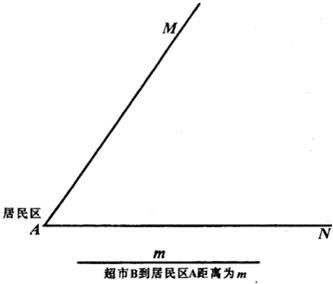20、如图，居民区A处有两条交义公路AM、AN，它们构成∠MAN．张三准备在∠MAN内部开一家超市B，李四准备在公路AM上开一家洗车场C．根据以下条件，请用尺规作图确定超市B及洗车场C的位置．（写出已知、求作，作图不写作法，但要求保留作图痕迹．）
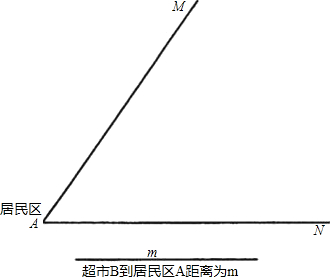、求作，作图不写作法，但要求保留作图痕迹．）