5、如图（1），在四边形木条框架中，任意加连1根对角线木条，就能使框架的形状稳定．
（1）判断下列说法是否正确（正确打“√”，错误打“×”）
①在图（2）中任意加连2根对角线木条，都能使框架的形状稳定；
②在图（3）中任意加连3根对角线木条，都能使框架的形状稳定．
（2）图（4）是一个用螺钉将木条连接成的框架，颇具美感，对于它的形状是否稳定，下面有四种判断，其中正确的是．
A、形状已经是稳定的
B、至少还要加连一根木条才能稳定
C、至少还要加连两根木条才能稳定
D、至少还要加连三根木条才能稳定

如图（1），在四边形木条框架中，任意加连1根对角线木条，就能使框架的形状稳定．


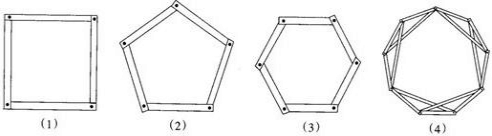
（1）判断下列说法是否正确（正确打“√”，错误打“×”）
①在图（2）中任意加连2根对角线木条，都能使框架的形状稳定______；
②在图（3）中任意加连3根对角线木条，都能使框架的形状稳定______．
（2）图（4）是一个用螺钉将木条连接成的框架，颇具美感，对于它的形状是否稳定，下面有四种判断，其中正确的是______．
A、形状已经是稳定的
B、至少还要加连一根木条才能稳定
C、至少还要加连两根木条才能稳定
D、至少还要加连三根木条才能稳定．

如图1，过△ABC顶点A作BC边上的高AD和中线AE，点D是垂足，点E是BC中点，规定λ_A=

DE

BE

．特别地，当D、E重合时，规定λ_A=0．另外对λ_B、λ_C也作类似规定．

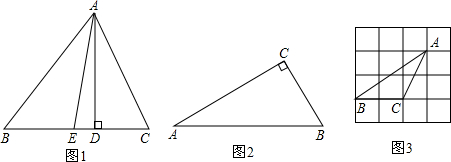
（1）①当△ABC中，AB=AC时，则λ_A=；②当△ABC中，λ_A=λ_B=0时，则△ABC的形状是；
（2）如图2，在Rt△ABC中，∠A=30°，求λ_A和λ_C的值；
（3）如图3，正方形网格中，格点△ABC的λ_A=；
（4）判断下列三种说法的正误（正确的打“√”错误的打“×”）
①若△ABC中λ_A＜1，则△ABC为锐角三角形；
②若△ABC中λ_A=1，则△ABC为直角三角形；
③若△ABC中λ_A＞1，则△ABC为钝角三角形；
（5）通过本题解答，同学们应该有这样的认识：一个无论多么陌生、多么综合的问题，其实都来自于书本已学的基础知识．因此，我们今后应重视基础知识的学习；同时在解决问题时或者解决问题后，应该思考该问题的本质和目的：①巩固哪些基础知识；②培养我们哪些方面能力；③向我们渗透哪些数学思想．本题之所以是一道综合题，就是因为涉及到的知识点多、面广．下面就请你谈谈本题中所用到的、已学过的性质、定理、公理或判定等．（至少列举两条）