摘要：21．(成志班的附加题.不计入总分)已知函数 (1)函数的图象是否为中心对称图形?若是.指出其对称中心, (2)当 (3)利用函数.令在上述构造数列的过程中.如果在定义域中.构造数列的过程继续下去.否则.如不在定义域中.则构造数列的过程停止.①如果可以用上述方法构造一个常数列.求出实数a的范围,②如果取定义域中的任何一个.都可以用上述方法构造一个无穷数列.求实数a的值.
网址：http://m.1010jiajiao.com/timu_id_23161[举报]
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
选项
C
C
D
C
D
C
B
B
C
A
二、填空题
11． 12． 13．必要不充分 14．5 15． 16．③
三、解答题
17．解：（1）令
令
（2）
（同上，）
18．（普通班）
解：设二次函数
又
符合
（2）
18．（成志班）
解：（1） ①
②
①―②得
而
数列为首项，2为公比的比数列
（2）
（3）由于
当
当
当
又
同上：
19．解（1）（2）
（3）
用错项相减 得
（4）
而
设f1(x)=
，定义fn+1(x)=f1[fn(x)]，an=
，n∈N*．
（1）写出an+1与an的关系式；
（2）数列{an}的通项公式；
（3）若T2n=2a2+4a4+6a6+…+2na2n，求T2n．
（4）（只限成志班学生做）若
=
，n∈N+，试比较9T2n与Qn的大小，并说明理由．
查看习题详情和答案>>
| 2 |
| 1+x |
| fn(0)-1 |
| fn(0)+2 |
（1）写出an+1与an的关系式；
（2）数列{an}的通项公式；
（3）若T2n=2a2+4a4+6a6+…+2na2n，求T2n．
（4）（只限成志班学生做）若
| Q | n |
| 4n2+n |
| 4n2+4n+1 |
设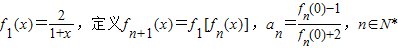
．
（1）写出an+1与an的关系式；
（2）数列{an}的通项公式；
（3）若T2n=2a2+4a4+6a6+…+2na2n，求T2n．
（4）（只限成志班学生做）若
的大小，并说明理由．
查看习题详情和答案>>
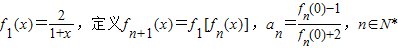．（1）写出an+1与an的关系式；
（2）数列{an}的通项公式；
（3）若T2n=2a2+4a4+6a6+…+2na2n，求T2n．
（4）（只限成志班学生做）若
的大小，并说明理由．查看习题详情和答案>>
．
的大小，并说明理由．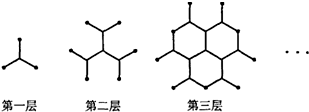
（2013•宁德模拟）一种平面分形图的形成过程如图所示，第一层是同 一点出发的三条线段，长度均为1，每两条线段夹角为 120°；第二层是在第一层的每一条线段末端，再生成 两条与该线段成120°角的线段，长度不变；第三层按 第二层的方法再在第二层每一条线段的末端各生成两条 线段；重复前面的作法，直至第6层，则分形图第6层 各条线段末端之间的距离的最大值为
成等比数列”是“
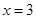”的