摘要:17.定义域在R上的函数对于任意的且 当 (1)判断并证明函数的单调性和奇偶性, (2)解不等式:
网址:http://m.1010jiajiao.com/timu_id_23156[举报]
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
选项
C
C
D
C
D
C
B
B
C
A
二、填空题
11. 12. 13.必要不充分 14.5 15. 16.③
三、解答题
17.解:(1)令
令
(2)
(同上,)
18.(普通班)
解:设二次函数
又
符合
(2)
18.(成志班)
解:(1) ①
②
①―②得
而
数列为首项,2为公比的比数列
(2)
(3)由于
当
当
当
又
同上:
19.解(1)(2)
(3)
用错项相减 得
(4)
而
定义域在R上的函数f(x)对于任意的x,y有f(x+y)=f(x)+f(y)成立,且f(2)=3,当x>0时,f(x)>0.
(1)判断并证明函数f(x)的单调性和奇偶性;
(2)解不等式:f(|x-5|)-6<f(|2x+3|).
查看习题详情和答案>>
(1)判断并证明函数f(x)的单调性和奇偶性;
(2)解不等式:f(|x-5|)-6<f(|2x+3|).
定义域在R上的函数f(x)对于任意的x,y有f(x+y)=f(x)+f(y)成立,且f(2)=3,当x>0时,f(x)>0.
(1)判断并证明函数f(x)的单调性和奇偶性;
(2)解不等式:f(|x-5|)-6<f(|2x+3|).
查看习题详情和答案>>
定义域在R上的函数f(x)对于任意的x,y有f(x+y)=f(x)+f(y)成立,且f(2)=3,当x>0时,f(x)>0.
(1)判断并证明函数f(x)的单调性和奇偶性;
(2)解不等式:f(|x-5|)-6<f(|2x+3|).
查看习题详情和答案>>
(1)判断并证明函数f(x)的单调性和奇偶性;
(2)解不等式:f(|x-5|)-6<f(|2x+3|).
查看习题详情和答案>>
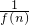 ,bn=f(
,bn=f( )+1
)+1