摘要：19．函数f(x)定义域为[0.4].其图象关于x=2对称.若f(x)在[0.2]为减函数时.解不等式f(x)＜f(4-2x)
网址：http://m.1010jiajiao.com/timu_id_23134[举报]
一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
C
D
D
A
C
A
A
D
C
C
A
二、填空题：本大题共4小题，每小题4分，共16分，把答案填在横线上。
13． 10 14．
15．
①②③ 16． 8
三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤。
17．
18．（1）x>1或x<－1
（2）a>1时，
0<a≤1/2时，不存在
1/2<a<1时，
19． f (2+x) = f (2－x) ∴f (4-2x) = f (2x)
0≤2x≤2，即0≤x≤1，无解
2≤2x≤4,即1≤x≤2，由f (x)<f (4-2x)得4/3<x≤2
20．P1=11/12 P2=13/36
21．
22．（1）
（2）
设函数f（x）定义域为R，对一切x、y∈R，均满足：f（x+y）+f（x-y）=2f（x）cosy，且f（0）=3，f(
)=4，
（1）求f（π）的值；
（2）求证：f（x）为周期函数，并求出其一个周期；
（3）求函数f（x）解析式． 查看习题详情和答案>>
| π | 2 |
（1）求f（π）的值；
（2）求证：f（x）为周期函数，并求出其一个周期；
（3）求函数f（x）解析式． 查看习题详情和答案>>
设函数f（x）定义域为R，对一切x、y∈R，均满足：f（x+y）+f（x-y）=2f（x）cosy，且f（0）=3，f(
)=4，
（1）求f（π）的值；
（2）求证：f（x）为周期函数，并求出其一个周期；
（3）求函数f（x）解析式．
查看习题详情和答案>>
| π |
| 2 |
（1）求f（π）的值；
（2）求证：f（x）为周期函数，并求出其一个周期；
（3）求函数f（x）解析式．
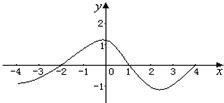
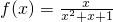；（5）f（x）=2x-1；其中是β函数的序号是________．