摘要:因为.PA=PB, 但AB≠PA.所以以A.P.B.Q为顶点的菱形的顶点D只能在PD的延长线上().延长PD至点Q,使DQ=PQ.由DQ=PQ.AD=DB.且PDAB 得菱形APBQ.但PQ=2PD=大于半径PA.所以.点P在⊙P外.即在⊙P上不否存在点Q.使以A.P.B.Q为顶点的四边形是菱形().
网址:http://m.1010jiajiao.com/timu_id_215219[举报]
(2012•晋江市质检)把一块三角板置于平面直角坐标系中,三角板的直角顶点为P,两直角边与x轴交于A、B,如图1,测得PA=PB,AB=2.以P为顶点的抛物线y=-(x-2)2+k恰好经过A、B两点,抛物线的对称轴x=a与x轴交于点E.
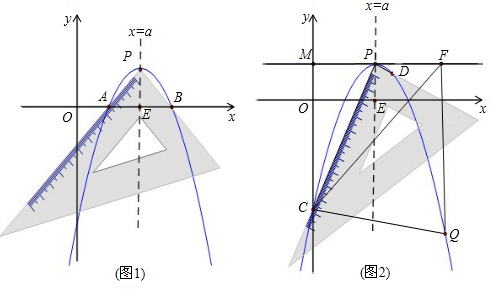
(1)填空:a=
(2)设抛物线与y轴交于点C,过P作直线PM⊥y轴,垂足为M.如图2,把三角板绕着点P旋转一定角度,使其中一条直角边恰好过点C,另一条直角边与抛物线的交点为D,试问:点C、D、E三点是否在同一直线上?请说明理由.
(3)在(2)的条件下,若Q(m,n)为抛物线上的一动点,连接CF、QC,过Q作QF⊥PM,垂足为F.试探索:是否存在点Q,使得△QCF是以QC为腰的等腰三角形?若存在,请求出m的值;若不存在,请说明理由.
查看习题详情和答案>>

(1)填空:a=
2
2
,k=1
1
,点E的坐标为(2,0)
(2,0)
;(2)设抛物线与y轴交于点C,过P作直线PM⊥y轴,垂足为M.如图2,把三角板绕着点P旋转一定角度,使其中一条直角边恰好过点C,另一条直角边与抛物线的交点为D,试问:点C、D、E三点是否在同一直线上?请说明理由.
(3)在(2)的条件下,若Q(m,n)为抛物线上的一动点,连接CF、QC,过Q作QF⊥PM,垂足为F.试探索:是否存在点Q,使得△QCF是以QC为腰的等腰三角形?若存在,请求出m的值;若不存在,请说明理由.
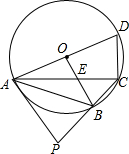 如图,四边形ABCD内接于⊙O,已知直径AD=2
如图,四边形ABCD内接于⊙O,已知直径AD=2| 3 |
(1)求CE:AE的值;
(2)在CB的延长线上取一点P,使PB=2BC,试判断直线PA和⊙O的位置关系,并证明你的结论;
(3)在(2)的情况下,求线段PA、PB与
 |
| AB |
(2012•连云港)已知梯形ABCD,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3,

问题1:如图1,P为AB边上的一点,以PD,PC为边作平行四边形PCQD,请问对角线PQ,DC的长能否相等,为什么?
问题2:如图2,若P为AB边上一点,以PD,PC为边作平行四边形PCQD,请问对角线PQ的长是否存在最小值?如果存在,请求出最小值,如果不存在,请说明理由.
问题3:若P为AB边上任意一点,延长PD到E,使DE=PD,再以PE,PC为边作平行四边形PCQE,请探究对角线PQ的长是否也存在最小值?如果存在,请求出最小值,如果不存在,请说明理由.
问题4:如图3,若P为直线DC上任意一点,延长PA到E,使AE=nPA(n为常数),以PE、PB为边作平行四边形PBQE,请探究对角线PQ的长是否也存在最小值?如果存在,请求出最小值,如果不存在,请说明理由.
查看习题详情和答案>>

问题1:如图1,P为AB边上的一点,以PD,PC为边作平行四边形PCQD,请问对角线PQ,DC的长能否相等,为什么?
问题2:如图2,若P为AB边上一点,以PD,PC为边作平行四边形PCQD,请问对角线PQ的长是否存在最小值?如果存在,请求出最小值,如果不存在,请说明理由.
问题3:若P为AB边上任意一点,延长PD到E,使DE=PD,再以PE,PC为边作平行四边形PCQE,请探究对角线PQ的长是否也存在最小值?如果存在,请求出最小值,如果不存在,请说明理由.
问题4:如图3,若P为直线DC上任意一点,延长PA到E,使AE=nPA(n为常数),以PE、PB为边作平行四边形PBQE,请探究对角线PQ的长是否也存在最小值?如果存在,请求出最小值,如果不存在,请说明理由.
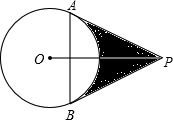 如图,已知PA、PB切⊙O于A、B两点,连接AB,且PA、PB的长是方程
如图,已知PA、PB切⊙O于A、B两点,连接AB,且PA、PB的长是方程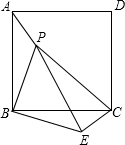 已知:如图所示,P是正方形ABCD内一点,且PA=1,PB=2,PC=3,以B为旋转中心,将△ABP按顺时针方向旋转到△CBE位置,AB边与CB边重合,则∠APB=∠CEB=
已知:如图所示,P是正方形ABCD内一点,且PA=1,PB=2,PC=3,以B为旋转中心,将△ABP按顺时针方向旋转到△CBE位置,AB边与CB边重合,则∠APB=∠CEB=