网址:http://m.1010jiajiao.com/timu_id_214196[举报]
2.下列等式中,一定成立的是
(A) ;
(B)
;
(B) ;
;
(C) ;
(D)
;
(D) .
.
3. 是下列哪个方程的解
是下列哪个方程的解
(A) ;
(B)
;
(B) ;
;
(C) ;
(D)
;
(D) .
.
4.已知点A (-2,3 )在双曲线 上,则下列点中,一定在该双曲线上的点是
上,则下列点中,一定在该双曲线上的点是
(A)A (3,-2 ); (B)A (-2,-3 ); (C)A (2,3 ); (D)A (3,2) .
5.下列图形中,是旋转对称图形,但不是中心对称图形的是
(A)等腰梯形; (B)等边三角形; (C)平行四边形; (D)直角梯形.
6.在研究圆的有关性质时,我们曾做过这样的一个操作“将一张圆形纸片沿着它的任意一条 直径翻折,可以看到直径两侧的两个半圆互相重合”。由此说明:
(A)圆是中心对称图形,圆心是它的对称中心;
(B)圆是轴对称图形,任意一条直径所在的直线都是它的对称轴;
(C)圆的直径互相平分;
(D)垂直弦的直径平分弦及弦所对的弧.
一、填空题:(本大题共12题,每题4分,满分48分)
 [请将结果直接填入答题纸的相应位置]
[请将结果直接填入答题纸的相应位置]
7.计算: = ▲ .
= ▲ .
8.因式分解: =
▲ .
=
▲ .
9.方程 的解为 ▲ .
的解为 ▲ .
10.已知一次函数y=kx+b的图象经过点A(2,1)(如图1), 当x ▲ 时,y≥1.
11.从1、2、3、…… 9九个自然数中任选一个数,选出的数被2整除的概率是 ▲ .
12.小明家离开学校的距离是a米,他上学时每分钟走b米,放学回家时每分钟比上学时少走
13.请你写出一个二次函数解析式,使其图像的顶点在 轴上,且在
轴上,且在 轴右侧图像是下降的。 ________▲________.
轴右侧图像是下降的。 ________▲________.
14.已知长方形ABCD,AB =3,BC =1,则 ____▲____.
____▲____.
15.已知⊙ 的半径为3,⊙
的半径为3,⊙ 的半径为2,若⊙
的半径为2,若⊙ 与⊙
与⊙ 相切,则
相切,则 、
、 的距离为 ▲ .
的距离为 ▲ .
16.已知向量 ,
, ,且
,且 ,则向量
,则向量 = ▲ .
= ▲ .
17.小强站在外滩黄浦江边观测对面的东方明珠电视塔,测得塔顶的仰角为 ,塔底的俯角为
,塔底的俯角为 ,如果王强离电视塔的距离为
,如果王强离电视塔的距离为 米,则电视塔的高度为 ▲ 米(用所给字母表示)。
米,则电视塔的高度为 ▲ 米(用所给字母表示)。
18.已知RT△ABC中,∠ACB =90°,AC =6,BC = 8,点D是AB中点,点E是直线AC上一点,若以C、D、E为顶点的三角形与△ABC相似,则AE的长度为 ▲ .
三、解答题:(本大题共7题,满分78分)
19.(本题满分10分)
解方程: 
20.(本题满分10分,第(1)小题满分5分,第(2)小题满分5分)
已知一次函数 图像与y轴的交点位于y轴负半轴上,且函数值y随自变量x的增大而减小。
图像与y轴的交点位于y轴负半轴上,且函数值y随自变量x的增大而减小。
 (1)求m的取值范围;
(1)求m的取值范围;
(2)又如果该一次函数的图像与坐标轴围成的三角形面积
是2,求这个一次函数的解析式。
21.(本题满分10分,第(1)小题满分6分,第(2)小题满分4分)
如图,D是射线AB上一点,过点D作DE∥AC,交∠BAC平分线于点E,过点D作
DF⊥AE ,垂足为F,DF交AC于点G.
(1)按要求在所给图中将图形补全,然后判断四边形ADEG的形状,并证明你的结论;
 (2)标出有向线段
(2)标出有向线段 、
、 、
、 ,记向量
,记向量 、
、 ,
,
试用 表示向量
表示向量 。
。
|
 已知被调查居民每户每月的用水量在
已知被调查居民每户每月的用水量在 之间,被调查的居民中对居民用水价格调价幅度抱“无所谓”态度的有8户,试回答下列问题:
之间,被调查的居民中对居民用水价格调价幅度抱“无所谓”态度的有8户,试回答下列问题:
 (含
(含 )
) (2)若⊙
(2)若⊙ ,
,  ,求CD的长。
,求CD的长。

 ,经过点A、
,经过点A、 与
与 轴的交点的纵坐标为2.
轴的交点的纵坐标为2. (2)设该抛物线的顶点为点P,点B的坐标为
(2)设该抛物线的顶点为点P,点B的坐标为 ,且
,且 ,若△ABP是等腰三角形,求点B的坐标。
,若△ABP是等腰三角形,求点B的坐标。

 (3)如果把条件中的“EG⊥FH”改为“EG与FH的夹角为45°”,并假设正方形ABCD的边长为1,FH的长为
(3)如果把条件中的“EG⊥FH”改为“EG与FH的夹角为45°”,并假设正方形ABCD的边长为1,FH的长为 (如图10),试求EG的长度。
(如图10),试求EG的长度。

 7.
7. ; 8.
; 9.
; 8.
; 9. ; 10.
; 10. ; 11. ;
; 11. ; 等; 14.3; 15.5或1; 16.4;
等; 14.3; 15.5或1; 16.4; ; 18.3或
; 18.3或 ;
; …………………………(3分)
…………………………(3分) …………………………(1分)
…………………………(1分)  …………………………(2分)
…………………………(2分)  …………………………(2分)
…………………………(2分)  是原方程的根,
是原方程的根, 是增根;…………………………(2分)
是增根;…………………………(2分) 。
。  即
即
 即
…………………………(2分)
即
…………………………(2分)
 ∴
…………………………(1分)
∴
…………………………(1分) 与x轴的交点为
…………………(1分)
与x轴的交点为
…………………(1分) 
 …………………………(1分)
…………………………(1分) 不合,舍去
不合,舍去 …………………………(1分)
…………………………(1分) …………………………(1分)
…………………………(1分) ∵ DE∥AC
∵ DE∥AC
 ∠DAE=∠EAC
∠DAE=∠EAC 根据题意,得:
根据题意,得: ……………(1分)
……………(1分) ……………(2分)
……………(2分) …………………(1分)
…………………(1分)

 的居民调价后用水费用的增长幅度不超过50%
的居民调价后用水费用的增长幅度不超过50% 时,水费的增长幅度为
时,水费的增长幅度为  ……(1分)
……(1分) 时,
时, …………………………(1分)
…………………………(1分) …………………………(1分)
…………………………(1分) …(1分)
…(1分) 、
、 ,垂足分别为点E、F
,垂足分别为点E、F ∵
∵ 是连心线,AB是公共弦
是连心线,AB是公共弦 …………………(1分)
…………………(1分) …………………(1分)
…………………(1分)

 …………………(1分)
…………………(1分)


 …………………(1分)
…………………(1分)
 …………………(1分)
…………………(1分) …………………(2分)
…………………(2分) …………………(1分)
…………………(1分) 得P(1,3)
得P(1,3)  ……………(1分)
……………(1分)  ,即
,即  ………………(1分)
………………(1分) …………………(1分)
…………………(1分)
 ……………………………………(1分)
……………………………………(1分) 不合题意舍去,∴
不合题意舍去,∴ …………………(1分)
…………………(1分)
 ……………………………………(1分)
……………………………………(1分) 时,△ABP是等腰三角形.
时,△ABP是等腰三角形. ∴∠NAM=90°
∴∠NAM=90° ∠BAM=∠DAN
∠BAM=∠DAN ∴AM=HF AN=EG
∴AM=HF AN=EG 的平方根是
的平方根是

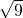 的平方根是________,(-3)2的平方根是________.若
的平方根是________,(-3)2的平方根是________.若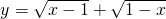 ,则x2012+2012y=________.
,则x2012+2012y=________. B ±
B ±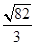
 的平方根是( )
的平方根是( )