摘要:⑶请根据上面的结论猜想:椭圆的“左特征点 是怎样的点?并证明你的结论.
网址:http://m.1010jiajiao.com/timu_id_21229[举报]
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
B
C
C
A
C
B
C
C
B
B
C
二、填空题
13.( ) 14.x=0或y=0 15.4 16.2/3 17.20 18.①④
) 14.x=0或y=0 15.4 16.2/3 17.20 18.①④
三、解答题
19.解:A(―4,2)关于直线 :
: 对称的点为
对称的点为 ,因为直线
,因为直线 是
是 中
中 的平分线,可以点
的平分线,可以点 在直线
在直线 上,故直线
上,故直线 的方程是
的方程是 ,由
,由 ,
, ,则
,则 是以
是以 为直角的三角形,
为直角的三角形, ,
, 10
10
20.解:由 ,
, ,设双曲线方程为
,设双曲线方程为 ,椭圆方程为
,椭圆方程为 ,它们的焦点
,它们的焦点 ,则
,则

 ,又
,又 ,
, ,
, 双曲线方程为
双曲线方程为 ,椭圆方程为
,椭圆方程为
21.解: ,设椭圆方程为
,设椭圆方程为 ①,设过
①,设过 和
和 的直线方程为
的直线方程为 ②,将②代入①得
②,将②代入①得 -
- ③,设
③,设 ,
, 的中点为
的中点为
 代入
代入 ,
, ,
, ,由③
,由③
 ,
, ,解得
,解得
22.解:⑴设直线 方程为:
方程为: 代入
代入 ,得
,得
 ,另知直线
,另知直线 与半圆相交的条件为
与半圆相交的条件为 ,设
,设 ,则
,则 ,
, ,点
,点 位于
位于 的右侧,应有
的右侧,应有 ,即
,即 ,
, (亦可求出
(亦可求出 的横坐标
的横坐标 )
)
⑵若 为正
为正 ,则点
,则点 到直线
到直线 距离
距离


 与
与 矛盾,
矛盾, 在⑴条件下不可能是正△.
在⑴条件下不可能是正△.
 23.⑴由题意设椭圆方程为:
23.⑴由题意设椭圆方程为: ,则
,则 解得:
解得:  ,所以椭圆方程为:
,所以椭圆方程为:
⑵设“左特征点” ,设
,设 ,
, 为
为 的平分线,
的平分线, ,
, ,下面设直线
,下面设直线 的方程为
的方程为 ,代入
,代入 得:
得: ,
, 代入上式得
代入上式得 解得
解得
⑶椭圆 的“左特征点”M是椭圆的左准线和x轴的交点证明如下:
的“左特征点”M是椭圆的左准线和x轴的交点证明如下:
证明:设椭圆的左准线 与x轴相交于点M,过点A、B分别作
与x轴相交于点M,过点A、B分别作 的垂线,垂足分别为点C、D。据椭圆第二定义得
的垂线,垂足分别为点C、D。据椭圆第二定义得 ,
,
∵ ∥
∥ ∥
∥ ,∴
,∴ ,
,
∴ ∵
∵ 与
与 均为锐角,∴
均为锐角,∴ 。
。
∴ 。∴
。∴ 为
为 的平分线。故点
的平分线。故点 为椭圆的“左特征点”。
为椭圆的“左特征点”。
为了减少碳排放量,某工厂进行技术改造,改造后生产甲产品 过程中记录产量x(吨)与相应的煤消耗量y(吨)数据如下表:
(1)请画出上表数据的散点图;
(2)请根据上面的数据,求出y关于x的线性回归方程
=bx+a;
(3)已知该厂技术改造前10吨甲产品需要煤12吨,试根据第二问求出的线性回归方程,预测生产10吨甲产品需要煤比技改前降低多少吨煤?
查看习题详情和答案>>
| X | 3 | 4 | 5 | 6 | ||||
| Y |
|
3 | 4 |
|
(2)请根据上面的数据,求出y关于x的线性回归方程
| ? |
| y |
(3)已知该厂技术改造前10吨甲产品需要煤12吨,试根据第二问求出的线性回归方程,预测生产10吨甲产品需要煤比技改前降低多少吨煤?
为了减少碳排放量,某工厂进行技术改造,改造后生产甲产品 过程中记录产量x(吨)与相应的煤消耗量y(吨)数据如下表:
(1)请画出上表数据的散点图;
(2)请根据上面的数据,求出y关于x的线性回归方程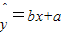 ;
;
(3)已知该厂技术改造前10吨甲产品需要煤12吨,试根据第二问求出的线性回归方程,预测生产10吨甲产品需要煤比技改前降低多少吨煤?
查看习题详情和答案>>
| X | 3 | 4 | 5 | 6 |
| Y |  | 3 | 4 |  |
(2)请根据上面的数据,求出y关于x的线性回归方程
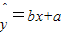 ;
;(3)已知该厂技术改造前10吨甲产品需要煤12吨,试根据第二问求出的线性回归方程,预测生产10吨甲产品需要煤比技改前降低多少吨煤?
查看习题详情和答案>>
设定义域为[x1,x2]的函数y=f(x)的图象为C,图象的两个端点分别为A、B,点O为坐标原点,点M是C上任意一点,向量
=(x1,y1),
=(x2,y2),
=(x,y),满足x=λx1+(1-λ)x2(0<λ<1),又有向量
=λ
+(1-λ)
,现定义“函数y=f(x)在[x1,x2]上可在标准k下线性近似”是指|
|≤k恒成立,其中k>0,k为常数.根据上面的表述,给出下列结论:①A、B、N三点共线;②“函数y=5x2在[0,1]上可在标准1下线性近似”; ③“函数y=5x2在[0,1]上可在标准
下线性近似”. 其中所有正确结论的序号为( )
| OA |
| OB |
| OM |
| ON |
| OA |
| OB |
| MN |
| 5 |
| 4 |
| A、①、② | B、②、③ |
| C、①、③ | D、①、②、③ |
有甲乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,
得到如下的列联表:
已知在全部105人中抽到随机抽取1人为优秀的概率为
(Ⅰ)请完成上面的列联表;
(Ⅱ)根据列联表的数据,若按95%的可靠性要求,能否认为“成绩与班级有关系”;
(Ⅲ)若按下面的方法从甲班优秀的学生抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到6或10号的概率. 查看习题详情和答案>>
得到如下的列联表:
| 优秀 | 非优秀 | 总计 | |
| 甲班 | 10 | ||
| 乙班 | 30 | ||
| 合计 | 105 |
| 2 |
| 7 |
(Ⅰ)请完成上面的列联表;
(Ⅱ)根据列联表的数据,若按95%的可靠性要求,能否认为“成绩与班级有关系”;
(Ⅲ)若按下面的方法从甲班优秀的学生抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到6或10号的概率. 查看习题详情和答案>>
(2012•海口模拟)衡阳市第一次联考后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,得到如下的2×2列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为
.
(1)请完成上面的列联表;
(2)根据列联表的数据,若按99.9%的可靠性要求,能否认为“成绩与班级有关系”;
(3)若按下面的方法从甲班优秀的学生中抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到9号或10号的概率.
参考公式与临界值表:K2=
.
查看习题详情和答案>>
| 3 |
| 11 |
| 优秀 | 非优秀 | 合计 | |
| 甲班 | 10 | ||
| 乙班 | 30 | ||
| 合计 | 110 |
(2)根据列联表的数据,若按99.9%的可靠性要求,能否认为“成绩与班级有关系”;
(3)若按下面的方法从甲班优秀的学生中抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到9号或10号的概率.
参考公式与临界值表:K2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |