网址:http://m.1010jiajiao.com/timu_id_20510[举报]
近年来,某市为了促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱。为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1000吨生活垃圾,数据统计如下(单位:吨):
|
|
“厨余垃圾”箱 |
“可回收物”箱 |
“其他垃圾”箱 |
|
厨余垃圾 |
400 |
100 |
100 |
|
可回收物 |
30 |
240 |
30 |
|
其他垃圾 |
20 |
20 |
60 |
(Ⅰ)试估计厨余垃圾投放正确的概率
(Ⅱ)试估计生活垃圾投放错误的概率
(Ⅲ)假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为a,b,c,其中a>0,a+b+c=600.当数据a,b,c,的方差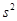 最大时,写出a,b,c的值(结论不要求证明),并求此时
最大时,写出a,b,c的值(结论不要求证明),并求此时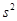 的值。
的值。
(注: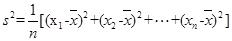 ,其中
,其中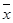 为数据
为数据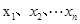 的平均数)
的平均数)
【解析】(1)厨余垃圾投放正确的概率约为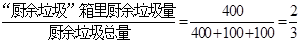
(2)设生活垃圾投放错误为事件A,则事件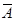 表示生活垃圾投放正确。事件
表示生活垃圾投放正确。事件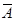 的概率约为“厨余垃圾”箱里厨余垃圾量、“可回收物”箱里可回收物量与“其他垃圾”箱里其他垃圾量的总和除以生活垃圾总量,即
的概率约为“厨余垃圾”箱里厨余垃圾量、“可回收物”箱里可回收物量与“其他垃圾”箱里其他垃圾量的总和除以生活垃圾总量,即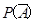 约为
约为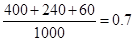 ,所以
,所以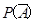 约为
约为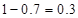
(3)当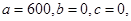 时,方差取得最大值,因为
时,方差取得最大值,因为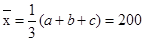 ,
,
所以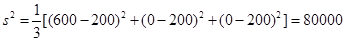
查看习题详情和答案>>
设A是由m×n个实数组成的m行n列的数表,满足:每个数的绝对值不大于1,且所有数的和为零,记s(m,n)为所有这样的数表构成的集合。
对于A∈S(m,n),记ri(A)为A的第ⅰ行各数之和(1≤ⅰ≤m),Cj(A)为A的第j列各数之和(1≤j≤n):
记K(A)为∣r1(A)∣,∣R2(A)∣,…,∣Rm(A)∣,∣C1(A)∣,∣C2(A)∣,…,∣Cn(A)∣中的最小值。
(1) 对如下数表A,求K(A)的值;
|
1 |
1 |
-0.8 |
|
0.1 |
-0.3 |
-1 |
(2)设数表A∈S(2,3)形如
|
1 |
1 |
c |
|
a |
b |
-1 |
求K(A)的最大值;
(3)给定正整数t,对于所有的A∈S(2,2t+1),求K(A)的最大值。
【解析】(1)因为 ,
,
所以
(2) 不妨设 .由题意得
.由题意得 .又因为
.又因为 ,所以
,所以 ,
,
于是 ,
, ,
,

所以 ,当
,当 ,且
,且 时,
时, 取得最大值1。
取得最大值1。
(3)对于给定的正整数t,任给数表 如下,
如下,
|
|
|
… |
|
|
|
|
… |
|
任意改变A的行次序或列次序,或把A中的每一个数换成它的相反数,所得数表
 ,并且
,并且 ,因此,不妨设
,因此,不妨设 ,
,
且
 。
。
由 得定义知,
得定义知, ,
,

又因为
所以


所以,
对数表 :
:
|
1 |
1 |
… |
1 |
|
… |
|
|
|
|
… |
|
-1 |
… |
-1 |
则 且
且 ,
,
综上,对于所有的 ,
, 的最大值为
的最大值为
查看习题详情和答案>>
近年来,某市为了促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱。为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1000吨生活垃圾,数据统计如下(单位:吨):
|
|
“厨余垃圾”箱 |
“可回收物”箱 |
“其他垃圾”箱 |
|
厨余垃圾 |
400 |
100 |
100 |
|
可回收物 |
30 |
240 |
30 |
|
其他垃圾 |
20 |
20 |
60 |
(Ⅰ)试估计厨余垃圾投放正确的概率
(Ⅱ)试估计生活垃圾投放错误的概率
(Ⅲ)假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为a,b,c,其中a>0,a+b+c=600.当数据a,b,c,的方差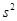 最大时,写出a,b,c的值(结论不要求证明),并求此时
最大时,写出a,b,c的值(结论不要求证明),并求此时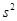 的值。
的值。
(注: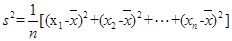 ,其中
,其中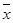 为数据
为数据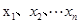 的平均数)
的平均数)
【解析】(1)厨余垃圾投放正确的概率约为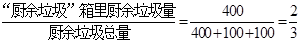
(2)设生活垃圾投放错误为事件A,则事件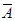 表示生活垃圾投放正确。事件
表示生活垃圾投放正确。事件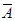 的概率约为“厨余垃圾”箱里厨余垃圾量、“可回收物”箱里可回收物量与“其他垃圾”箱里其他垃圾量的总和除以生活垃圾总量,即
的概率约为“厨余垃圾”箱里厨余垃圾量、“可回收物”箱里可回收物量与“其他垃圾”箱里其他垃圾量的总和除以生活垃圾总量,即 约为
约为 ,所以
,所以 约为
约为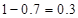
(3)当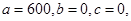 时,方差取得最大值,因为
时,方差取得最大值,因为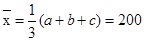 ,
,
所以
查看习题详情和答案>>
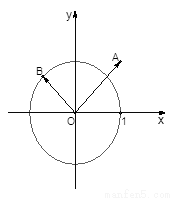
如图,已知点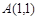 和单位圆上半部分上的动点B.
和单位圆上半部分上的动点B.
(1)若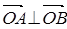 ,求向量
,求向量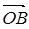 ;
;
(2)求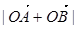 的最大值.
的最大值.
【解析】对于这样的向量的坐标和模最值的求解,利用建立直角坐标系的方法可知。
第一问中,依题意,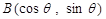 ,
,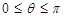
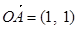 ,
,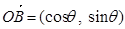
因为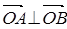 ,所以
,所以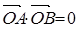 ,即
,即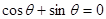 ,
,
解得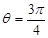 ,所以
,所以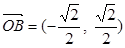
第二问中,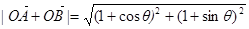 结合三角函数的性质得到最值。
结合三角函数的性质得到最值。
(1)依题意,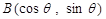 ,
,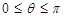 (不含1个或2个端点也对)
(不含1个或2个端点也对)
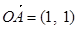 ,
,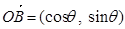 (写出1个即可)
(写出1个即可)
因为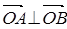 ,所以
,所以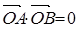 ,即
,即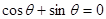 ,
,
解得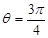 ,所以
,所以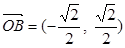 .-
.-
(2)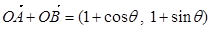 ,
,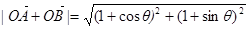
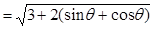
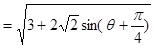 当
当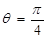 时,
时,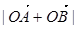 取得最大值,
取得最大值,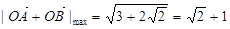
查看习题详情和答案>>
设A是如下形式的2行3列的数表,
|
a |
b |
c |
|
d |
e |
f |
满足性质P:a,b,c,d,e,f ,且a+b+c+d+e+f=0
,且a+b+c+d+e+f=0
记 为A的第i行各数之和(i=1,2),
为A的第i行各数之和(i=1,2),  为A的第j列各数之和(j=1,2,3)记
为A的第j列各数之和(j=1,2,3)记 为
为 中的最小值。
中的最小值。
(1)对如下表A,求 的值
的值
|
1 |
1 |
-0.8 |
|
0.1 |
-0.3 |
-1 |
(2)设数表A形如
|
1 |
1 |
-1-2d |
|
d |
d |
-1 |
其中 ,求
,求 的最大值
的最大值
(3)对所有满足性质P的2行3列的数表A,求 的最大值。
的最大值。
【解析】(1)因为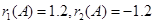 ,
, ,所以
,所以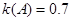
(2)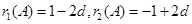 ,
,
因为 ,所以
,所以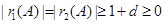 ,
,
所以
当d=0时, 取得最大值1
取得最大值1
(3)任给满足性质P的数表A(如图所示)
|
a |
b |
c |
|
d |
e |
f |
任意改变A的行次序或列次序,或把A中的每个数换成它的相反数,所得数表 仍满足性质P,并且
仍满足性质P,并且 ,因此,不妨设
,因此,不妨设 ,
, ,
,
由 得定义知,
得定义知, ,
, ,
, ,
,
从而

所以, ,由(2)知,存在满足性质P的数表A使
,由(2)知,存在满足性质P的数表A使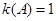 ,故
,故 的最大值为1
的最大值为1
【考点定位】此题作为压轴题难度较大,考查学生分析问题解决问题的能力,考查学生严谨的逻辑思维能力
查看习题详情和答案>>







