摘要：由 . ① 得. ∴过点P的切线的斜率k切=2.
网址：http://m.1010jiajiao.com/timu_id_20134[举报]
设椭圆C：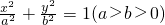
的左、右焦点分别为F1，F2，上顶点为A，以F1为圆心F1F2为半径的圆恰好经过点A且与直线l：x-
y-3=0相切
（1）求椭圆C的离心率；
（2）求椭圆C的方程；
（3）过右焦点F2作斜率为K的直线与椭圆C交于M、N两点，在x轴上是否存在点P（m，0）使得PM，PN以为邻边的平行四边形是菱形，如果存在，求出m的取值范围，如果不存在，说明理由．
查看习题详情和答案>>
设椭圆C：
+
=1(a＞b＞0)的左、右焦点分别为F1，F2，上顶点为A，以F1为圆心F1F2为半径的圆恰好经过点A且与直线l：x-
y-3=0相切
（1）求椭圆C的离心率；
（2）求椭圆C的方程；
（3）过右焦点F2作斜率为K的直线与椭圆C交于M、N两点，在x轴上是否存在点P（m，0）使得PM，PN以为邻边的平行四边形是菱形，如果存在，求出m的取值范围，如果不存在，说明理由．
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
（1）求椭圆C的离心率；
（2）求椭圆C的方程；
（3）过右焦点F2作斜率为K的直线与椭圆C交于M、N两点，在x轴上是否存在点P（m，0）使得PM，PN以为邻边的平行四边形是菱形，如果存在，求出m的取值范围，如果不存在，说明理由．
设点P是曲线C：x2=2py（p＞0）上的动点，点P到点（0，1）的距离和它到焦点F的距离之和的最小值为
．
（1）求曲线C的方程；
（2）若点P的横坐标为1，过P作斜率为k（k≠0）的直线交C于点Q，交x轴于点M，过点Q且与PQ垂直的直线与C交于另一点N，问是否存在实数k，使得直线MN与曲线C相切？若存在，求出k的值；若不存在，请说明理由．
查看习题详情和答案>>
| 5 | 4 |
（1）求曲线C的方程；
（2）若点P的横坐标为1，过P作斜率为k（k≠0）的直线交C于点Q，交x轴于点M，过点Q且与PQ垂直的直线与C交于另一点N，问是否存在实数k，使得直线MN与曲线C相切？若存在，求出k的值；若不存在，请说明理由．
．