摘要：(四川省成都市高2009届高中毕业班第一次诊断性检测)已知函数f.当x∈[1.3]时.函数f(x)的取值范围恰为[-.]的解析式,.＝(k2+k+2.3k+1).解关于x的不等式f(x)＜?解: ∵a＞0.c＜0.∴f '＞0 ∴函数f(x)在[1.3]上是增函数 --3' 由 Þ a＝2.c＝-4 ∴f --5' (2)∵?＝- --6' ∴f(x)＜? ó ＜- ó ＜ ó ＜0 ó ＜0 --8' ∵k＞-1.且k≠0.∴k+1＞0 于是-1＜k＜0时.x∈ 0＜k＜1时.x∈ k＝1时.x∈ k＞1时.x∈ --12'
网址：http://m.1010jiajiao.com/timu_id_198154[举报]
.
； 
在
上最大值和最小值
的离心率为 
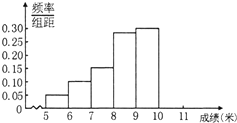某市为了了解今年高中毕业生的身体素质状况，从本市某校高中毕业班中抽取一个班进行实心球测试，成绩在8米及以上的为合格．把所得数据进行整理后，分成6组画出频率分布直方图的一部分（如图），已知第一小组为[5，6），从左到右前5个小组的频率分别为0.06，0.1，0.14，0.28，0.3．第6小组的频数是6．（Ⅰ）求这次实心球测试成绩合格的人数；
（Ⅱ）经过多次测试后，甲成绩在8～10米之间，乙成绩在9.5～10.5米之间，现甲、乙各投一次，求乙投得没有甲远的概率．
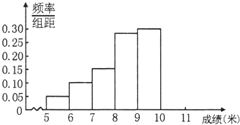（2012•湛江二模）某市为了解今年高中毕业生的身体素质状况，从本市某校高中毕业班中抽取一个班进行实心球测试，成绩在8米及以上的为合格．把所得数据进行整理后，分成6组画出频率分布直方图的一部分（如图），已知第一小组为[5，6），从左到右前5个小组的频率分别为0.06，0.10，0.14，0.28，0.30．第6小组的频数是6．（1）求这次实心球测试成绩合格的人数；
（2）用此次测试结果估计全市毕业生的情况．若从今年的高中毕业生中随机抽取两名，记X表示两人中成绩不合格的人数，求X的分布列及数学期望；
（3）经过多次测试后，甲成绩在8～10米之间，乙成绩在9.5～10.5米之间，现甲、乙各投一次，求甲投得比乙远的概率．