网址:http://m.1010jiajiao.com/timu_id_196296[举报]
已知向量 (
( ),向量
),向量 ,
, ,
,
且

 .
.
(Ⅰ)求向量 ;
(Ⅱ)若
;
(Ⅱ)若 ,
, ,求
,求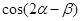 .
.
【解析】本试题主要考查了向量的数量积的运算,以及两角和差的三角函数关系式的运用。
(1)问中∵ ,∴
,∴ ,…………………1分
,…………………1分
∵ ,得到三角关系是
,得到三角关系是 ,结合
,结合 ,解得。
,解得。
(2)由 ,解得
,解得 ,
, ,结合二倍角公式
,结合二倍角公式 ,和
,和 ,代入到两角和的三角函数关系式中就可以求解得到。
,代入到两角和的三角函数关系式中就可以求解得到。
解析一:(Ⅰ)∵ ,∴
,∴ ,…………1分
,…………1分
∵ ,∴
,∴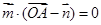 ,即
,即 ① …………2分
① …………2分
又 ② 由①②联立方程解得,
② 由①②联立方程解得,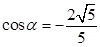 ,
,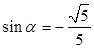 5分
5分
∴ ……………6分
……………6分
(Ⅱ)∵ 即
即 ,
, , …………7分
, …………7分
∴ ,
, ………8分
………8分
又∵ , ………9分
, ………9分
 , ……10分
, ……10分
∴ .
.
解法二: (Ⅰ) ,…………………………………1分
,…………………………………1分
又 ,∴
,∴ ,即
,即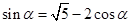 ,①……2分
,①……2分
又 ②
②
将①代入②中,可得 ③ …………………4分
③ …………………4分
将③代入①中,得 ……………………………………5分
……………………………………5分
∴ …………………………………6分
…………………………………6分
(Ⅱ) 方法一
∵ ,
, ,∴
,∴ ,且
,且 ……7分
……7分
∴ ,从而
,从而 . …………………8分
. …………………8分
由(Ⅰ)知 ,
,
 ; ………………9分
; ………………9分
∴ . ………………………………10分
. ………………………………10分
又∵ ,∴
,∴ ,
又
,
又 ,∴
,∴ ……11分
……11分
综上可得  ………………………………12分
………………………………12分
方法二∵ ,
, ,∴
,∴ ,且
,且 …………7分
…………7分
∴ .
……………8分
.
……………8分
由(Ⅰ)知 ,
, .
…………9分
.
…………9分
∴ ……………10分
……………10分
∵ ,且注意到
,且注意到 ,
,
∴ ,又
,又 ,∴
,∴ ………………………11分
………………………11分
综上可得  …………………12分
…………………12分
(若用 ,又∵
,又∵ ∴
∴  ,
,
查看习题详情和答案>>
设椭圆 的左、右顶点分别为
的左、右顶点分别为 ,点
,点 在椭圆上且异于
在椭圆上且异于 两点,
两点, 为坐标原点.
为坐标原点.
(Ⅰ)若直线 与
与 的斜率之积为
的斜率之积为 ,求椭圆的离心率;
,求椭圆的离心率;
(Ⅱ)若 ,证明直线
,证明直线 的斜率
的斜率
 满足
满足
【解析】(1)解:设点P的坐标为 .由题意,有
.由题意,有 ①
①
由 ,得
,得 ,
,
由 ,可得
,可得 ,代入①并整理得
,代入①并整理得
由于 ,故
,故 .于是
.于是 ,所以椭圆的离心率
,所以椭圆的离心率
(2)证明:(方法一)
依题意,直线OP的方程为 ,设点P的坐标为
,设点P的坐标为 .
.
由条件得 消去
消去 并整理得
并整理得 ②
②
由 ,
, 及
及 ,
,
得 .
.
整理得 .而
.而 ,于是
,于是 ,代入②,
,代入②,
整理得
由 ,故
,故 ,因此
,因此 .
.
所以 .
.
(方法二)
依题意,直线OP的方程为 ,设点P的坐标为
,设点P的坐标为 .
.
由P在椭圆上,有
因为 ,
, ,所以
,所以 ,即
,即 ③
③
由 ,
, ,得
,得 整理得
整理得 .
.
于是 ,代入③,
,代入③,
整理得
解得 ,
,
所以 .
.
查看习题详情和答案>>
将函数![]() 的图象向左平移
的图象向左平移![]() 个单位,得到函数
个单位,得到函数![]() 即
即![]() 的图象,再向上平移1个单位,所得图象的函数解析式为
的图象,再向上平移1个单位,所得图象的函数解析式为![]() ,故选B.
,故选B.
答案:B
【命题立意】:本题考查三角函数的图象的平移和利用诱导公式及二倍角公式进行化简解析式的基本知识和基本技能,学会公式的变形. w.w.w.k.s.5.u.c.o.m
查看习题详情和答案>>已知 是等差数列,其前n项和为Sn,
是等差数列,其前n项和为Sn, 是等比数列,且
是等比数列,且 ,
, .
.
(Ⅰ)求数列 与
与 的通项公式;
的通项公式;
(Ⅱ)记 ,
, ,证明
,证明 (
( ).
).
【解析】(1)设等差数列 的公差为d,等比数列
的公差为d,等比数列 的公比为q.
的公比为q.
由 ,得
,得 ,
, ,
, .
.
由条件,得方程组 ,解得
,解得
所以 ,
, ,
, .
.
(2)证明:(方法一)
由(1)得
 ①
①
 ②
②
由②-①得



而
故 ,
,
(方法二:数学归纳法)
① 当n=1时,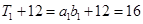 ,
, ,故等式成立.
,故等式成立.
② 假设当n=k时等式成立,即 ,则当n=k+1时,有:
,则当n=k+1时,有:






即 ,因此n=k+1时等式也成立
,因此n=k+1时等式也成立
由①和②,可知对任意 ,
, 成立.
成立.
查看习题详情和答案>>
已知递增等差数列 满足:
满足: ,且
,且 成等比数列.
成等比数列.
(1)求数列 的通项公式
的通项公式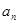 ;
;
(2)若不等式 对任意
对任意 恒成立,试猜想出实数
恒成立,试猜想出实数 的最小值,并证明.
的最小值,并证明.
【解析】本试题主要考查了数列的通项公式的运用以及数列求和的运用。第一问中,利用设数列 公差为
公差为 ,
,
由题意可知 ,即
,即 ,解得d,得到通项公式,第二问中,不等式等价于
,解得d,得到通项公式,第二问中,不等式等价于 ,利用当
,利用当 时,
时, ;当
;当 时,
时, ;而
;而 ,所以猜想,
,所以猜想, 的最小值为
的最小值为 然后加以证明即可。
然后加以证明即可。
解:(1)设数列 公差为
公差为 ,由题意可知
,由题意可知 ,即
,即 ,
,
解得 或
或 (舍去). …………3分
(舍去). …………3分
所以, . …………6分
. …………6分
(2)不等式等价于 ,
,
当 时,
时, ;当
;当 时,
时, ;
;
而 ,所以猜想,
,所以猜想, 的最小值为
的最小值为 . …………8分
. …………8分
下证不等式 对任意
对任意 恒成立.
恒成立.
方法一:数学归纳法.
当 时,
时, ,成立.
,成立.
假设当 时,不等式
时,不等式 成立,
成立,
当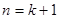 时,
时, ,
…………10分
,
…………10分
只要证  ,只要证
,只要证  ,
,
只要证  ,只要证
,只要证  ,
,
只要证  ,显然成立.所以,对任意
,显然成立.所以,对任意 ,不等式
,不等式 恒成立.…14分
恒成立.…14分
方法二:单调性证明.
要证 
只要证  ,
,
设数列 的通项公式
的通项公式 , …………10分
, …………10分
 , …………12分
, …………12分
所以对 ,都有
,都有 ,可知数列
,可知数列 为单调递减数列.
为单调递减数列.
而 ,所以
,所以 恒成立,
恒成立,
故 的最小值为
的最小值为 .
.
查看习题详情和答案>>