摘要:3.函数图象之间的变换通过作图体现性质.归结出底数a的变化情况对函数值的影响体验函数式的表达功能.感受实际问题与数学问题的转化.加深对数形结合的认识[教学重点]:指数函数的图象[教学难点]:指数函数的图象.以及图象的变换
网址:http://m.1010jiajiao.com/timu_id_194167[举报]
一元二次不等式的解集与一元二次方程的根及二次函数图象之间的关系分类列表如下:
约定:Δ=b2-4ac,a≠0,x1<x2.?
Δ的符号 | a的符号
| ax2+bx+c>0 | ax2+bx+c<0 | ||
解 集 | 图 象 | 解 集 | 图 象 | ||
Δ<0
| a>0 |
|
|
|
|
a<0 |
|
|
|
| |
Δ=0
| a>0 |
|
|
|
|
a<0 |
|
|
|
| |
Δ>0
| a>0 |
|
|
|
|
a<0 |
|
|
|
| |
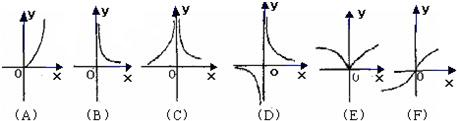
下面六个幂函数的图象如图所示,试建立函数与图象之间的对应关系.( )
(1)y=x
;(2)y=x
;(3)y=x
;(4)y=x-2;(5)y=x-3;(6)y=x-
.
(1)y=x
| 3 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |

| A、(1)?(A),(2)?(F),(3)?(E),(4)?(C),(5)?(D),(6)?(B) |
| B、(1)?(B),(2)?(E),(3)?(C),(4)?(D),(5)?(A),(6)?(F) |
| C、(1)?(A),(2)?(E),(3)?(B),(4)?(D),(5)?(C),(6)?(F) |
| D、(1)?(B),(2)?(F),(3)?(A),(4)?(C),(5)?(D),(6)?(E) |