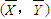摘要：的条件下.若在区间内总存在个实数.使得不等式成立.求的最大值．
网址：http://m.1010jiajiao.com/timu_id_193078[举报]
下列四个命题：
①f（a）f（b）＜0为函数f（x）在区间（a，b）内存在零点的必要不充分条件；
②命题“?x∈R，ex-2sinx+4≤0”的否定是“?x∉R，ex-2sinx+4＞0”
③从总体中抽取的样本（x1，y1），（x2，y2），…，（xn，yn）．若记
=
xi，
=
yi，则回归直线
=bx+a必过点(
，
)
④若关于x的不等式|x-1|+|x|＞m的解集为{x|x＜-1，或x＞2}，则m=3．
其中真命题的序号为 （写出所有正确的命题）
查看习题详情和答案>>
①f（a）f（b）＜0为函数f（x）在区间（a，b）内存在零点的必要不充分条件；
②命题“?x∈R，ex-2sinx+4≤0”的否定是“?x∉R，ex-2sinx+4＞0”
③从总体中抽取的样本（x1，y1），（x2，y2），…，（xn，yn）．若记
. |
| X |
| 1 |
| n |
| n |
 |
| i=1 |
. |
| Y |
| 1 |
| n |
| n |
|
| i=1 |
| ? |
| y |
. |
| X |
. |
| Y |
④若关于x的不等式|x-1|+|x|＞m的解集为{x|x＜-1，或x＞2}，则m=3．
其中真命题的序号为
下列四个命题：
①f（a）f（b）＜0 为函数f（x）在区间（a，b）内存在零点的必要不充分条件；
②从总体中抽取的样本（x1，y1），（x2，y2），…，（xa，ya），若记
=
∑xi，
=
∑yi，则回归直线
=bx+a必过点（
，
）；
③设点P是△ABC所在平面内的一点，且
+
=2
，则P为线段AC的中点；
④若空间两点A（1，2，-1），B（2，0，m）的距离为
，则m=2．
其中真命题的个数为（ ）
①f（a）f（b）＜0 为函数f（x）在区间（a，b）内存在零点的必要不充分条件；
②从总体中抽取的样本（x1，y1），（x2，y2），…，（xa，ya），若记
. |
| X |
| 1 |
| n |
. |
| Y |
| 1 |
| n |
| ? |
| y |
. |
| X |
. |
| Y |
③设点P是△ABC所在平面内的一点，且
| BC |
| BA |
| BP |
④若空间两点A（1，2，-1），B（2，0，m）的距离为
| 14 |
其中真命题的个数为（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
下列四个命题：
①f（a）f（b）＜0 为函数f（x）在区间（a，b）内存在零点的必要不充分条件；
②从总体中抽取的样本（x1，y1），（x2，y2），…，（xa，ya），若记
=
∑xi，
=
∑yi，则回归直线
必过点（
，
）；
③设点P是△ABC所在平面内的一点，且
，则P为线段AC的中点；
④若空间两点A（1，2，-1），B（2，0，m）的距离为
，则m=2．
其中真命题的个数为（ ）
A．1个
B．2个
C．3个
D．4个
查看习题详情和答案>>
①f（a）f（b）＜0 为函数f（x）在区间（a，b）内存在零点的必要不充分条件；
②从总体中抽取的样本（x1，y1），（x2，y2），…，（xa，ya），若记
=∑xi，=∑yi，则回归直线必过点（，）；③设点P是△ABC所在平面内的一点，且
，则P为线段AC的中点；④若空间两点A（1，2，-1），B（2，0，m）的距离为
，则m=2．其中真命题的个数为（ ）
A．1个
B．2个
C．3个
D．4个
查看习题详情和答案>>
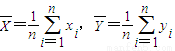，则回归直线
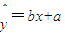必过点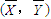
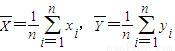，则回归直线
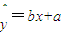必过点