摘要:故当时.有.
网址:http://m.1010jiajiao.com/timu_id_193007[举报]
已知函数 =
= .
.
(Ⅰ)当 时,求不等式
时,求不等式
 ≥3的解集;
≥3的解集;
(Ⅱ) 若 ≤
≤ 的解集包含
的解集包含 ,求
,求 的取值范围.
的取值范围.
【命题意图】本题主要考查含绝对值不等式的解法,是简单题.
【解析】(Ⅰ)当 时,
时, =
= ,
,
当 ≤2时,由
≤2时,由 ≥3得
≥3得 ,解得
,解得 ≤1;
≤1;
当2< <3时,
<3时, ≥3,无解;
≥3,无解;
当 ≥3时,由
≥3时,由 ≥3得
≥3得 ≥3,解得
≥3,解得 ≥8,
≥8,
∴ ≥3的解集为{
≥3的解集为{ |
| ≤1或
≤1或 ≥8};
≥8};
(Ⅱ)  ≤
≤
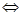
 ,
,
当 ∈[1,2]时,
∈[1,2]时, =
= =2,
=2,
∴ ,有条件得
,有条件得 且
且 ,即
,即 ,
,
故满足条件的 的取值范围为[-3,0]
的取值范围为[-3,0]
查看习题详情和答案>>
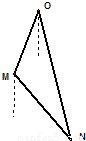
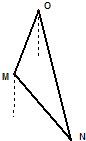 如图所示,正在亚丁湾执行护航任务的某导弹护卫舰,突然收到一艘商船的求救信号,紧急前往相关海域.到达相关海域O处后发现,在南偏西20°、5海里外的洋面M处有一条海盗船,它正以每小时20海里的速度向南偏东40°的方向逃窜.某导弹护卫舰当即施放载有突击队员的快艇进行拦截,快艇以每小时30海里的速度向南偏东θ°的方向全速追击.请问:快艇能否追上海盗船?如果能追上,请求出sin(θ°+20°)的值;如果未能追上,请说明理由.(假设海面上风平浪静、海盗船逃窜的航向不变、快艇运转正常无故障等)
查看习题详情和答案>>
如图所示,正在亚丁湾执行护航任务的某导弹护卫舰,突然收到一艘商船的求救信号,紧急前往相关海域.到达相关海域O处后发现,在南偏西20°、5海里外的洋面M处有一条海盗船,它正以每小时20海里的速度向南偏东40°的方向逃窜.某导弹护卫舰当即施放载有突击队员的快艇进行拦截,快艇以每小时30海里的速度向南偏东θ°的方向全速追击.请问:快艇能否追上海盗船?如果能追上,请求出sin(θ°+20°)的值;如果未能追上,请说明理由.(假设海面上风平浪静、海盗船逃窜的航向不变、快艇运转正常无故障等)
查看习题详情和答案>>
如图所示,正在亚丁湾执行护航任务的某导弹护卫舰,突然收到一艘商船的求救信号,紧急前往相关海域.到达相关海域O处后发现,在南偏西20°、5海里外的洋面M处有一条海盗船,它正以每小时20海里的速度向南偏东40°的方向逃窜.某导弹护卫舰当即施放载有突击队员的快艇进行拦截,快艇以每小时30海里的速度向南偏东θ°的方向全速追击.请问:快艇能否追上海盗船?如果能追上,请求出sin(θ°+20°)的值;如果未能追上,请说明理由.(假设海面上风平浪静、海盗船逃窜的航向不变、快艇运转正常无故障等)
 查看习题详情和答案>>
查看习题详情和答案>>
 查看习题详情和答案>>
查看习题详情和答案>>