摘要:由已知―2.4是方程的两个实数
网址:http://m.1010jiajiao.com/timu_id_192923[举报]
已知函数f(x)=
(x≠0)是奇函数,且满足f(1)=f(4)
(Ⅰ)求实数a、b的值;
(Ⅱ)试证明函数f(x)在区间(0,2]单调递减,在区间(2,+∞)单调递增;
(Ⅲ)是否存在实数k同时满足以下两个条件:
①不等式f(x)+
>0对x∈(0,+∞)恒成立;
②方程f(x)=k在x∈[-6,-1]上有解.若存在,试求出实数k的取值范围,若不存在,请说明理由.
查看习题详情和答案>>
| x2+ax+b |
| x |
(Ⅰ)求实数a、b的值;
(Ⅱ)试证明函数f(x)在区间(0,2]单调递减,在区间(2,+∞)单调递增;
(Ⅲ)是否存在实数k同时满足以下两个条件:
①不等式f(x)+
| k |
| 2 |
②方程f(x)=k在x∈[-6,-1]上有解.若存在,试求出实数k的取值范围,若不存在,请说明理由.
已知函数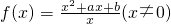 是奇函数,且满足f(1)=f(4)
是奇函数,且满足f(1)=f(4)
(Ⅰ)求实数a、b的值;
(Ⅱ)试证明函数f(x)在区间(0,2]单调递减,在区间(2,+∞)单调递增;
(Ⅲ)是否存在实数k同时满足以下两个条件:
①不等式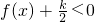 对x∈(0,+∞)恒成立;
对x∈(0,+∞)恒成立;
②方程f(x)=k在x∈[-6,-1]上有解.若存在,试求出实数k的取值范围,若不存在,请说明理由.
查看习题详情和答案>>
已知函数 (x≠0)是奇函数,且满足f(1)=f(4),
(x≠0)是奇函数,且满足f(1)=f(4),
(Ⅰ)求实数a、b的值;
(Ⅱ)试证明函数f(x)在区间(0,2]单调递减,在区间(2,+∞)单调递增;
(Ⅲ)是否存在实数k同时满足以下两个条件:①不等式f(x)+ <0对x∈(0,+∞)恒成立;②方程f(x)=k在x∈[-6,-1]上有解;若存在,试求出实数k的取值范围,若不存在,请说明理由。
<0对x∈(0,+∞)恒成立;②方程f(x)=k在x∈[-6,-1]上有解;若存在,试求出实数k的取值范围,若不存在,请说明理由。
查看习题详情和答案>>
 (x≠0)是奇函数,且满足f(1)=f(4),
(x≠0)是奇函数,且满足f(1)=f(4),(Ⅰ)求实数a、b的值;
(Ⅱ)试证明函数f(x)在区间(0,2]单调递减,在区间(2,+∞)单调递增;
(Ⅲ)是否存在实数k同时满足以下两个条件:①不等式f(x)+
 <0对x∈(0,+∞)恒成立;②方程f(x)=k在x∈[-6,-1]上有解;若存在,试求出实数k的取值范围,若不存在,请说明理由。
<0对x∈(0,+∞)恒成立;②方程f(x)=k在x∈[-6,-1]上有解;若存在,试求出实数k的取值范围,若不存在,请说明理由。  是奇函数,且满足f(1)=f(4)
是奇函数,且满足f(1)=f(4)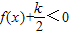 对x∈(0,+∞)恒成立;
对x∈(0,+∞)恒成立;