(Ⅱ)由(x1+x2)2-4x1x2＝4得+＝4, ∴b＝-3a3+9a2, ∴b¢＝-9a2+18a,由b¢＝0得a＝0或a＝2.又0＜a£3, ∴当a变化时,b&c——青夏教育精英家教网——

摘要：(Ⅱ)由(x1+x2)2-4x1x2＝4得+＝4, ∴b＝-3a3+9a2, ∴b¢＝-9a2+18a,由b¢＝0得a＝0或a＝2.又0＜a£3, ∴当a变化时,b¢,b的变化情况如下表:a0(0,2)2(2,3)3b¢ +0- b0极大值12¯0∴0£b£12 4分(Ⅳ)∵x1＜x＜2, ∴x-x1＞0,x-x2-2＜0,又h(x)＝3a(x-x1)(x-x2)-6a(x-x1)＝3a(x-x1)[(x-x2)-2], ∴|h(x)|＝|3a(x-x1)[(x-x2)-2]|＝

网址：http://m.1010jiajiao.com/timu_id_192825[举报]

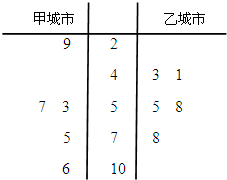（2013•朝阳区一模）国家环境标准制定的空气质量指数与空气质量等级对应关系如下表：

空气质量指数	0-50	51-100	101-150	151-200	201-300	300以上
空气质量等级	1级优	2级良	3级轻度污染	4级中度污染	5级重度污染	6级严重污染

由全国重点城市环境监测网获得2月份某五天甲城市和乙城市的空气质量指数数据用茎叶图表示如图：
（Ⅰ）试根据上面的统计数据，判断甲、乙两个城市的空气质量指数的方差的大小关系（只需写出结果）；
（Ⅱ）试根据上面的统计数据，估计甲城市某一天空气质量等级为2级良的概率；
（Ⅲ）分别从甲城市和乙城市的统计数据中任取一个，试求这两个城市空气质量等级相同的概率．
（注：s²=

）²+…+（x_n-

）²]，其中

为数据x₁，x₂，…，x_n的平均数．）

查看习题详情和答案>>

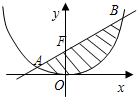如图，设由抛物线C：x²=4y与过它的焦点F的直线l所围成封闭曲面图形的面积为S（阴影部分）．
（1）设直线l与抛物线C交于两点A（x₁，y₁），B（x₂，y₂），且x₁＜x₂，直线l的斜率为k，试用k表示x₂-x₁；
（2）求S的最小值．查看习题详情和答案>>

设M是由满足下列条件的函数f（x）构成的集合：“①方程f（x）-x=0有实数根；②函数f（x）的导数f′（x）满足0＜f′（x）＜1．”
（Ⅰ）判断函数f(x)=

是否是集合M中的元素，并说明理由；
（Ⅱ）令g（x）=f（x）-x，判断g（x）的单调性（f（x）∈M）；
（Ⅲ）设x₁＜x₂，证明：0＜f（x₂）-f（x₁）＜x₂-x₁．

查看习题详情和答案>>

（2012•广东）由正整数组成的一组数据x₁，x₂，x₃，x₄，其平均数和中位数都是2，且标准差等于1，则这组数据为

．（从小到大排列）

查看习题详情和答案>>

A是由在[1，4]上有意义且满足如下条件的函数φ（x）组成的集合；
①对任意x∈[1，2]，都有φ（2x）∈（1，2）；
②存在常数L（0＜L＜1），使得对任意的x₁，x₂∈[1，2]都有|φ（2x₁）-φ（2x₂）|=L|x₁-x₂|
（1）设φ(x)=

，x∈[1，2]，证明：φ（x）∈A；
（2）设φ(x)=

，x∈[1，2]，是否存在设x₀∈（1，2），使得x₀=φ（2x₀），如存在，求出所有的x₀，如不存在请说明理由！查看习题详情和答案>>