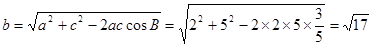∴且.即且.解得--5分——青夏教育精英家教网——

摘要：∴且.即且.解得--5分

网址：http://m.1010jiajiao.com/timu_id_192420[举报]

某市发行一种电脑彩票，从1到35这35个数中任选7个不同的数作为一注，开奖号码为从35个数中抽出7个不同的数，若购买的一注号码与这7个数字完全相同，即中一等奖；若购买的一注号码中有且仅有6个数与这7个数中的6个数字相同，即中二等奖；若购买的一注号码中有且仅有5个数与这7个数中的5个数字相同，即中三等奖．
（1）随机购买一注彩票中一等奖的概率是多少？随机购买一注彩票能中奖的概率是多少？（结果可以用含组合数的分数表示）
（2）从问题（1）得到启发，试判断组合数C_k^l•C_n-k^m-l与C_n^m的大小关系，并从组合的意义角度加以解释．

查看习题详情和答案>>

某市发行一种电脑彩票，从1到35这35个数中任选7个不同的数作为一注，开奖号码为从35个数中抽出7个不同的数，若购买的一注号码与这7个数字完全相同，即中一等奖；若购买的一注号码中有且仅有6个数与这7个数中的6个数字相同，即中二等奖；若购买的一注号码中有且仅有5个数与这7个数中的5个数字相同，即中三等奖．
（1）随机购买一注彩票中一等奖的概率是多少？随机购买一注彩票能中奖的概率是多少？（结果可以用含组合数的分数表示）
（2）从问题（1）得到启发，试判断组合数C_k^l•C_n-k^m-l与C_n^m的大小关系，并从组合的意义角度加以解释．
查看习题详情和答案>>

某产品生产厂家根据以往的生产销售经验得到下面有关生产销售的统计规律：每生产产品x（百台），其总成本为G（x）（万元），其中固定成本为2.8万元，并且每生产1百台的生产成本为1万元（总成本=固定成本+生产成本）．销售收入R（x）（万元）满足R(x)=

，假定该产品产销平衡（即生产的产品都能卖掉），根据上述统计规律，请完成下列问题：
（1）分别写出G（x）和利润函数y=f（x）的解析式（利润=销售收入-总成本）；
（2）工厂生产多少台产品时，可使盈利最多？并求出此时每台产品的售价．

查看习题详情和答案>>

已知点为圆上的动点，且不在轴上，轴，垂足为，线段中点的轨迹为曲线，过定点任作一条与轴不垂直的直线，它与曲线交于、两点。

（I）求曲线的方程；

（II）试证明：在轴上存在定点，使得总能被轴平分

【解析】第一问中设为曲线上的任意一点，则点在圆上，

∴，曲线的方程为

第二问中，设点的坐标为，直线的方程为，　　………………3分　　

代入曲线的方程，可得　

∵，∴

确定结论直线与曲线总有两个公共点．

然后设点,的坐标分别, ，则，

要使被轴平分，只要得到。

（1）设为曲线上的任意一点，则点在圆上，

∴，曲线的方程为． ………………2分

（2）设点的坐标为，直线的方程为，　　………………3分　　

代入曲线的方程，可得　，……5分

∵，∴，

∴直线与曲线总有两个公共点．（也可根据点M在椭圆的内部得到此结论）

………………6分

设点,的坐标分别, ，则，

要使被轴平分，只要， ………………9分

即，， ………………10分

也就是，，

即，即只要　 ………………12分　

当时，（＊）对任意的s都成立，从而总能被轴平分．

所以在x轴上存在定点，使得总能被轴平分

查看习题详情和答案>>

已知△的内角所对的边分别为且.

(1) 若, 求的值;

(2) 若△的面积求的值.

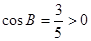【解析】本小题主要考查正弦定理、余弦定理、同角三角函数的基本关系等基础知识，考查运算求解能力。第一问中，得到正弦值，再结合正弦定理可知，，得到（2）中即所以c=5,再利用余弦定理，得到b的值。

解: (1)∵, 且, ∴ . 由正弦定理得， ∴.

(2)∵ ∴. ∴c=5

由余弦定理得，

∴

查看习题详情和答案>>