摘要： 已知平面直角坐标系上有6个点: A.D.F 下面有2个小题. (1)请将上述的6个点按下列的要求分成两类.并写出同类点具有而另一类点不具有的一个特征．(请将答案按下列要求写在横线上:特征不能用否定形式表述.点用字母表示．) ①甲类含两个点.乙类合其余四个点． 甲类:点 . 是同一类点.其特征是 ． 乙类:点 . . . .是同一类点.其特征是 ． ②甲类合三个点.乙类合其余三个点． 甲类:点 . . 是同一类点.其特征是 ． 乙类:点 . . 是同一类点.其特征是 ． (2)判断下列命题是否正确.正确的在括号内打“√ .并说明理由, 错误的在括号内打“× .并举反例说明． ①直线y＝-2x+11与线段AD没有交点( )(如需要.可在坐标系上作出示意图) ②直线y＝-2x+11将四边形ABCD分成面积相等的两部分．( )
网址：http://m.1010jiajiao.com/timu_id_19088[举报]
在平面直角坐标系xOy中，已知抛物线C1：y1=-x2+2x．（1）将抛物线C1先向右平移2个单位，再向上平移1个单位，得到抛物线C2，求抛物线C2的顶点P的坐标及它的解析式．
（2）如果x轴上有一动点M，那么在两条抛物线C1、C2上是否存在点N，使得以点O、P、M、N为顶点的四边形是平行四边形（OP为一边）？若存在，求出点N的坐标；若不存在，请说明理由．
在平面直角坐标系xOy中，已知抛物线C1：y1=-x2+2x．
（1）将抛物线C1先向右平移2个单位，再向上平移1个单位，得到抛物线C2，求抛物线C2的顶点P的坐标及它的解析式．
（2）如果x轴上有一动点M，那么在两条抛物线C1、C2上是否存在点N，使得以点O、P、M、N为顶点的四边形是平行四边形（OP为一边）？若存在，求出点N的坐标；若不存在，请说明理由．
查看习题详情和答案>>
在平面直角坐标系xOy中，已知抛物线C1：y1=-x2+2x．
（1）将抛物线C1先向右平移2个单位，再向上平移1个单位，得到抛物线C2，求抛物线C2的顶点P的坐标及它的解析式．
（2）如果x轴上有一动点M，那么在两条抛物线C1、C2上是否存在点N，使得以点O、P、M、N为顶点的四边形是平行四边形（OP为一边）？若存在，求出点N的坐标；若不存在，请说明理由．
查看习题详情和答案>>
（1）将抛物线C1先向右平移2个单位，再向上平移1个单位，得到抛物线C2，求抛物线C2的顶点P的坐标及它的解析式．
（2）如果x轴上有一动点M，那么在两条抛物线C1、C2上是否存在点N，使得以点O、P、M、N为顶点的四边形是平行四边形（OP为一边）？若存在，求出点N的坐标；若不存在，请说明理由．
查看习题详情和答案>>
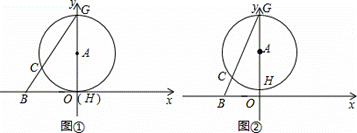
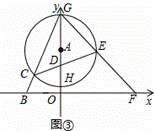
的⊙A交y轴于点G、H（点G在点H的上方），连接BG交⊙A于点C．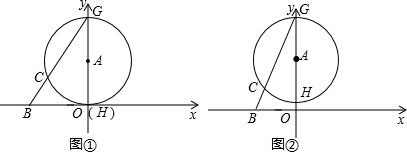
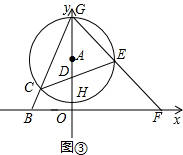
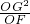的值不变；②OG•OF的值不变．其中有且只有一个结论是正确的，请你判断哪一个结论正确，证明正确的结论并求出其值．
的⊙A交y轴于点G、H（点G在点H的上方），连接BG交⊙A于点C．
时，求直线B
弦CE，连接GE并延长交x轴于点F，当⊙A与x轴相离时，给出下列结论：① 
的值不变；②OG•OF的值不变．其中有且只有一个结论是正确的，请你判断哪一个结论正确，写出正确的结论并直接写出其值．