(2)因为点R在直线m上的射影S满足所以PS⊥QS.即△PSQ是直角三角形.——青夏教育精英家教网——

摘要：(2)因为点R在直线m上的射影S满足所以PS⊥QS.即△PSQ是直角三角形.

网址：http://m.1010jiajiao.com/timu_id_183357[举报]

=1(a＞b＞0)的离心率为

．
（1）若圆（x-2）²+（y-1）²=

与椭圆相交于A、B两点且线段AB恰为圆的直径，求椭圆的方程；
（2）设L为过椭圆右焦点F的直线，交椭圆于M、N两点，且L的倾斜角为60°．求

的值．
（3）在（1）的条件下，椭圆W的左右焦点分别为F₁、F₂，点R在直线l：x-

y+8=0上．当∠F₁RF₂取最大值时，求

查看习题详情和答案>>

已知点A（-1，0）、B（1，0），△ABC的周长为2+2

．记动点C的轨迹为曲线W．
（1）直接写出W的方程（不写过程）；
（2）经过点（0，

）且斜率为k的直线l与曲线W 有两个不同的交点P和Q，是否存在常数k，使得向量

，1)共线？如果存在，求出k的值；如果不存在，请说明理由．
（3）设W的左右焦点分别为F₁、F₂，点R在直线l：x-

y+8=0上．当∠F₁RF₂取最大值时，求

查看习题详情和答案>>

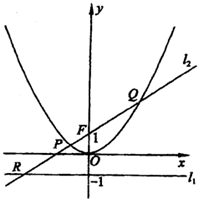已知定点F（0，1）和直线l₁：y=-1，过定点F与直线l₁相切的动圆圆心为点C．
（1）求动点C的轨迹方程；
（2）过点F在直线l₂交轨迹于两点P、Q，交直线l₁于点R，求

的最小值．查看习题详情和答案>>

曲线C是中心在原点，焦点在x轴上的双曲线的右支，已知它的右准线方程为l：x=

，一条渐近线方程是y=

x，线段PQ是过曲线C右焦点F的一条弦，R是弦PQ的中点．
（1）求曲线C的方程；
（2）当点P在曲线C上运动时，求点R到y轴距离的最小值；
（3）若在直线l的左侧能作出直线m：x=a，使点R在直线m上的射影S满足

=0．当点P在曲线C上运动时，求a的取值范围．

查看习题详情和答案>>

（08年龙岩一中冲刺文）（分）已知双曲线C的中心在原点，焦点在x轴上，右准线为一条渐近线的方程是过双曲线C的右焦点F₂的一条弦交双曲线右支于P、Q两点，R是弦PQ的中点.

（1）求双曲线C的方程；

（2）若A、B分别是双曲C上两条渐近线上的动点，且2|AB|=|F₁F₂|，求线段AB的中点M的迹方程，并说明该轨迹是什么曲线。

（3）若在双曲线右准线L的左侧能作出直线m:x=a，使点R在直线m上的射影S满足，当点P在曲线C上运动时，求a的取值范围.

查看习题详情和答案>>