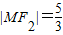摘要：椭圆E:,其右焦点为F.且．由圆Q与椭圆E的方程联立得2y2- 5kx + 20k- 30 = 0,
网址：http://m.1010jiajiao.com/timu_id_183192[举报]
在直角坐标系xOy中，椭圆C1：
+
=1(a＞b＞0)的左、右焦点分别为F1，F2．其中F2也是抛物线C2：y2=4x的焦点，点M为C1与C2在第一象限的交点，且|MF2|=
（Ⅰ）求C1的方程；
（Ⅱ）若过点D（4，0）的直线l与C1交于不同的两点E，F．E在DF之间，试求△ODE 与△ODF面积之比的取值范围．（O为坐标原点） 查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
| 5 |
| 3 |
（Ⅰ）求C1的方程；
（Ⅱ）若过点D（4，0）的直线l与C1交于不同的两点E，F．E在DF之间，试求△ODE 与△ODF面积之比的取值范围．（O为坐标原点） 查看习题详情和答案>>
在直角坐标系xOy中，椭圆C1：
+
=1(a＞b＞0)的左、右焦点分别为F1，F2．其中F2也是抛物线C2：y2=4x的焦点，点M为C1与C2在第一象限的交点，且|MF2|=
（Ⅰ）求C1的方程；
（Ⅱ）若过点D（4，0）的直线l与C1交于不同的两点E，F．E在DF之间，试求△ODE 与△ODF面积之比的取值范围．（O为坐标原点）
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
| 5 |
| 3 |
（Ⅰ）求C1的方程；
（Ⅱ）若过点D（4，0）的直线l与C1交于不同的两点E，F．E在DF之间，试求△ODE 与△ODF面积之比的取值范围．（O为坐标原点）
已知椭圆
+
=1(a＞b＞0)的右焦点为F，点E(
，0)在x轴上，若椭圆的离心率e=
，且|EF|=1．
（1）求a，b的值；
（2）若过F的直线交椭圆于A，B两点，且
+
与向量
=(4，-
)共线（其中O为坐标原点），求证：
与
的夹角为
．
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
| a2 |
| c |
| ||
| 2 |
（1）求a，b的值；
（2）若过F的直线交椭圆于A，B两点，且
| OA |
| OB |
| m |
| 2 |
| OA |
| OB |
| π |
| 2 |
的左、右焦点分别为F1，F2．其中F2也是抛物线C2：y2=4x的焦点，点M为C1与C2在第一象限的交点，且