摘要：解:(Ⅰ)动点的轨迹的方程为 , ------------3分
网址：http://m.1010jiajiao.com/timu_id_183008[举报]
已知曲线
上动点
到定点
与定直线
的距离之比为常数
．
（1）求曲线的轨迹方程；
（2）若过点
引曲线C的弦AB恰好被点
平分，求弦AB所在的直线方程；
（3）以曲线的左顶点
为圆心作圆：
，设圆与曲线交于点
与点
，求
的最小值，并求此时圆的方程.
【解析】第一问利用（1）过点
作直线
的垂线，垂足为D.
代入坐标得到
第二问当斜率k不存在时，检验得不符合要求；
当直线l的斜率为k时，
；，化简得
第三问点N与点M关于X轴对称，设
，， 不妨设
．
由于点M在椭圆C上，所以
．
由已知
，则
，
由于
，故当
时，
取得最小值为
．
计算得，
，故
，又点
在圆
上，代入圆的方程得到
．
故圆T的方程为：
查看习题详情和答案>>
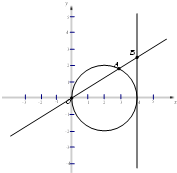（2011•南汇区二模）已知动直线y=kx交圆（x-2）2+y2=4于坐标原点O和点A，交直线x=4于点B，若动点M满足| OM |
| AB |
（1）试用k表示点A、点B的坐标；
（2）求动点M的轨迹方程F（x，y）=0；
（3）以下给出曲线C的五个方面的性质，请你选择其中的三个方面进行研究，并说明理由（若你研究的方面多于三个，我们将只对试卷解答中的前三项予以评分）．
①对称性；（2分）
②顶点坐标（定义：曲线与其对称轴的交点称为该曲线的顶点）；（2分）
③图形范围；（2分）
④渐近线；（3分）
⑤对方程F（x，y）=0，当y≥0时，函数y=f（x）的单调性．（3分）
已知动直线y=kx交圆（x-2）2+y2=4于坐标原点O和点A，交直线x=4于点B，若动点M满足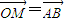
，动点M的轨迹C的方程为F（x，y）=0．
（1）试用k表示点A、点B的坐标；
（2）求动点M的轨迹方程F（x，y）=0；
（3）以下给出曲线C的五个方面的性质，请你选择其中的三个方面进行研究，并说明理由（若你研究的方面多于三个，我们将只对试卷解答中的前三项予以评分）．
①对称性；（2分）
②顶点坐标（定义：曲线与其对称轴的交点称为该曲线的顶点）；（2分）
③图形范围；（2分）
④渐近线；（3分）
⑤对方程F（x，y）=0，当y≥0时，函数y=f（x）的单调性．（3分）
查看习题详情和答案>>
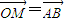，动点M的轨迹C的方程为F（x，y）=0．（1）试用k表示点A、点B的坐标；
（2）求动点M的轨迹方程F（x，y）=0；
（3）以下给出曲线C的五个方面的性质，请你选择其中的三个方面进行研究，并说明理由（若你研究的方面多于三个，我们将只对试卷解答中的前三项予以评分）．
①对称性；（2分）
②顶点坐标（定义：曲线与其对称轴的交点称为该曲线的顶点）；（2分）
③图形范围；（2分）
④渐近线；（3分）
⑤对方程F（x，y）=0，当y≥0时，函数y=f（x）的单调性．（3分）
查看习题详情和答案>>
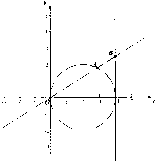已知点A（x1，y1）在圆（x-2）2+y2=4上运动，点A不与（0，0）重合，点B（4，y0）在直线x=4上运动，动点M（x，y）满足
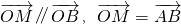．动点M的轨迹C的方程为F（x，y）=0．
．动点M的轨迹C的方程为F（x，y）=0．