网址:http://m.1010jiajiao.com/timu_id_160001[举报]
如图, 是△
是△ 的重心,
的重心, 、
、 分别是边
分别是边 、
、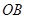 上的动点,且
上的动点,且 、
、 、
、 三点共线.
三点共线.
(1)设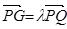 ,将
,将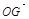 用
用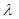 、
、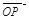 、
、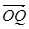 表示;
表示;
(2)设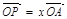 ,
,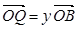 ,证明:
,证明: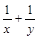 是定值;
是定值;
(3)记△ 与△
与△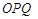 的面积分别为
的面积分别为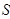 、
、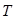 .求
.求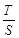 的取值范围.
的取值范围.
(提示: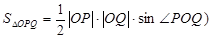
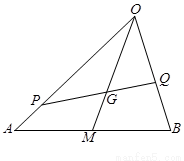
【解析】第一问中利用(1)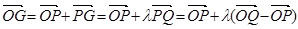
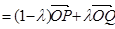
第二问中,由(1),得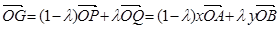 ;①
;①
另一方面,∵ 是△
是△ 的重心,
的重心,
∴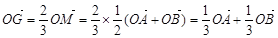
而 、
、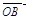 不共线,∴由①、②,得
不共线,∴由①、②,得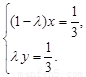
第三问中,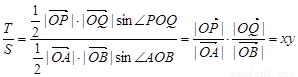
由点 、
、 的定义知
的定义知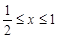 ,
,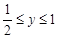 ,
,
且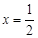 时,
时,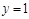 ;
;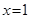 时,
时,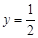 .此时,均有
.此时,均有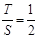 .
.
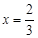 时,
时,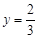 .此时,均有
.此时,均有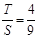 .
.
以下证明: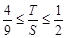 ,结合作差法得到。
,结合作差法得到。
解:(1)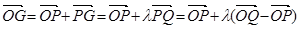
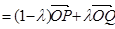 .
.
(2)一方面,由(1),得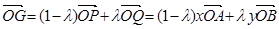 ;①
;①
另一方面,∵ 是△
是△ 的重心,
的重心,
∴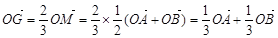 . ②
. ②
而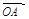 、
、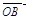 不共线,∴由①、②,得
不共线,∴由①、②,得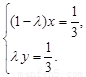
解之,得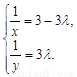 ,∴
,∴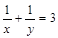 (定值).
(定值).
(3)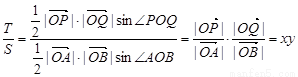 .
.
由点 、
、 的定义知
的定义知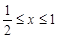 ,
,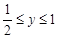 ,
,
且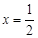 时,
时,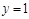 ;
;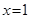 时,
时,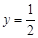 .此时,均有
.此时,均有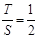 .
.
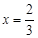 时,
时,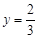 .此时,均有
.此时,均有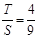 .
.
以下证明: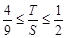 .(法一)由(2)知
.(法一)由(2)知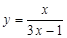 ,
,
∵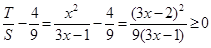 ,∴
,∴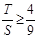 .
.
∵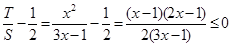 ,∴
,∴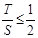 .
.
∴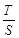 的取值范围
的取值范围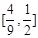
查看习题详情和答案>>
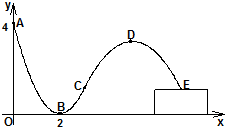 轮滑是穿着带滚轮的特制鞋在坚硬的场地上滑行的运动.如图,助跑道ABC是一段抛物线,某轮滑运动员通过助跑道获取速度后飞离跑道然后落到离地面高为1米的平台上E处,飞行的轨迹是一段抛物线CDE(抛物线CDE与抛物线ABC在同一平面内),D为这段抛物线的最高点.现在运动员的滑行轨迹所在平面上建立如图所示的直角坐标系,x轴在地面上,助跑道一端点A(0,4),另一端点C(3,1),点B(2,0),单位:米.
轮滑是穿着带滚轮的特制鞋在坚硬的场地上滑行的运动.如图,助跑道ABC是一段抛物线,某轮滑运动员通过助跑道获取速度后飞离跑道然后落到离地面高为1米的平台上E处,飞行的轨迹是一段抛物线CDE(抛物线CDE与抛物线ABC在同一平面内),D为这段抛物线的最高点.现在运动员的滑行轨迹所在平面上建立如图所示的直角坐标系,x轴在地面上,助跑道一端点A(0,4),另一端点C(3,1),点B(2,0),单位:米.(Ⅰ)求助跑道所在的抛物线方程;
(Ⅱ)若助跑道所在抛物线与飞行轨迹所在抛物线在点C处有相同的切线,为使运动员安全和空中姿态优美,要求运动员的飞行距离在4米到6米之间(包括4米和6米),试求运动员飞行过程中距离平台最大高度的取值范围?
(注:飞行距离指点C与点E的水平距离,即这两点横坐标差的绝对值.)
已知数列 的前
的前 项和为
项和为 ,且
,且 (
( N*),其中
N*),其中 .
.
(Ⅰ) 求 的通项公式;
的通项公式;
(Ⅱ) 设 (
( N*).
N*).
①证明:  ;
;
② 求证: .
.
【解析】本试题主要考查了数列的通项公式的求解和运用。运用 关系式,表示通项公式,然后得到第一问,第二问中利用放缩法得到
关系式,表示通项公式,然后得到第一问,第二问中利用放缩法得到 ,②由于
,②由于 ,
,
所以 利用放缩法,从此得到结论。
利用放缩法,从此得到结论。
解:(Ⅰ)当 时,由
时,由 得
得 . ……2分
. ……2分
若存在 由
由 得
得 ,
,
从而有 ,与
,与 矛盾,所以
矛盾,所以 .
.
从而由 得
得 得
得 . ……6分
. ……6分
(Ⅱ)①证明:
证法一:∵ ∴
∴
∴
∴ .…………10分
.…………10分
证法二: ,下同证法一.
……10分
,下同证法一.
……10分
证法三:(利用对偶式)设 ,
, ,
,
则 .又
.又 ,也即
,也即 ,所以
,所以 ,也即
,也即 ,又因为
,又因为 ,所以
,所以 .即
.即
 ………10分
………10分
证法四:(数学归纳法)①当 时,
时,  ,命题成立;
,命题成立;
②假设 时,命题成立,即
时,命题成立,即 ,
,
则当 时,
时,

 即
即
即
故当 时,命题成立.
时,命题成立.
综上可知,对一切非零自然数 ,不等式②成立. ………………10分
,不等式②成立. ………………10分
②由于 ,
,
所以 ,
,
从而 .
.
也即
查看习题详情和答案>>