摘要：当r∈>0. 4分因此,当半径r>2时,f′单调递增,即半径越大,利润越高;半径r<2时,f′单调递减,即半径越大,利润越低. 6分(1)半径为6 cm时,利润最大. 8分(2)半径为2 cm时,利润最小,这时f(2)<0,表示此种瓶内饮料的利润还不够瓶子的成本,此时利润是负值. 10分
网址：http://m.1010jiajiao.com/timu_id_15912[举报]
已知函数f1（x）=e|x-2a+1|，f2（x）=e|x-a|+1，x∈R．
（1）若a=2，求f（x）=f1（x）+f2（x）在x∈[2，3]上的最小值；
（2）若|f1（x）-f2（x）|=f2（x）-f1（x）对于任意的实数x∈R恒成立，求a的取值范围；
（3）当4≤a≤6时，求函数g（x）=
-
在x∈[1，6]上的最小值．
查看习题详情和答案>>
（1）若a=2，求f（x）=f1（x）+f2（x）在x∈[2，3]上的最小值；
（2）若|f1（x）-f2（x）|=f2（x）-f1（x）对于任意的实数x∈R恒成立，求a的取值范围；
（3）当4≤a≤6时，求函数g（x）=
| f1(x)+f2(x) |
| 2 |
| |f1(x)-f2(x)| |
| 2 |
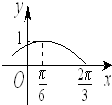（2013•长春一模）函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，-| π |
| 2 |
| π |
| 2 |
（1）求函数y=f（x）的解析式；
（2）当x∈[-π，-
| π |
| 6 |
是定义在R上的偶函数，且对任意
，都有
，当
[4，6]时，
，则函数
的值
为（ ） 
B．
D．
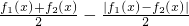在x∈[1，6]上的最小值．
x，定义数列{an}:a0=8,a1=10,an=f(an-1),n=1,2,…
an(n=1,2,…)；
)n(n∈N*).
成立；
成立.