摘要:=0,得a=. 3分
网址:http://m.1010jiajiao.com/timu_id_15899[举报]
设f(x)是定义在[a,b]上的函数,用分点T:a=x0<x1<…<xi-1<xi<…xn=b将区间[a,b]任意划分成n个小区间,如果存在一个常数M>0,使得和
|f(xi)-f(xi-1)|≤M(i=1,2,…,n)恒成立,则称f(x)为[a,b]上的有界变差函数.
(1)函数f(x)=x2在[0,1]上是否为有界变差函数?请说明理由;
(2)设函数f(x)是[a,b]上的单调递减函数,证明:f(x)为[a,b]上的有界变差函数;
(3)若定义在[a,b]上的函数f(x)满足:存在常数k,使得对于任意的x1、x2∈[a,b]时,|f(x1)-f(x2)|≤k•|x1-x2|.证明:f(x)为[a,b]上的有界变差函数. 查看习题详情和答案>>
查看习题详情和答案>>
| n |  | i=1 |
(1)函数f(x)=x2在[0,1]上是否为有界变差函数?请说明理由;
(2)设函数f(x)是[a,b]上的单调递减函数,证明:f(x)为[a,b]上的有界变差函数;
(3)若定义在[a,b]上的函数f(x)满足:存在常数k,使得对于任意的x1、x2∈[a,b]时,|f(x1)-f(x2)|≤k•|x1-x2|.证明:f(x)为[a,b]上的有界变差函数. 查看习题详情和答案>>
已知A(3,0)及双曲线E: -
- =1,若双曲线E的右支上的点Q到点B(m,0)(m≥3)距离的最小值为|AB|.?
=1,若双曲线E的右支上的点Q到点B(m,0)(m≥3)距离的最小值为|AB|.?
(1)求m的取值范围,并指出当m变化时点B的轨迹G.
(2)轨迹G上是否存在一点D,它在直线y=![]() x上的射影为P,使得
x上的射影为P,使得![]() ·
·![]() =
=![]() ·
·![]() ?若存在,试指出双曲线E的右焦点F分向量
?若存在,试指出双曲线E的右焦点F分向量![]() 所成的比;若不存在,请说明理由.
所成的比;若不存在,请说明理由.
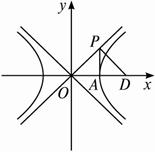
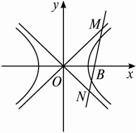
(3)当m为定值时,过轨迹G上的点B(m,0)作一条直线l与双曲线E的右支交于不同的两点,且与直线y=![]() x,y=-
x,y=-![]() x分别交于M,N两点,求△MON周长的最小值.
x分别交于M,N两点,求△MON周长的最小值.
设f(x)是定义在[a,b]上的函数,用分点T:a=x<x1<…<xi-1<xi<…xn=b将区间[a,b]任意划分成n个小区间,如果存在一个常数M>0,使得和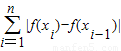 ≤M(i=1,2,…,n)恒成立,则称f(x)为[a,b]上的有界变差函数.
≤M(i=1,2,…,n)恒成立,则称f(x)为[a,b]上的有界变差函数.
(1)函数f(x)=x2在[0,1]上是否为有界变差函数?请说明理由;
(2)设函数f(x)是[a,b]上的单调递减函数,证明:f(x)为[a,b]上的有界变差函数;
(3)若定义在[a,b]上的函数f(x)满足:存在常数k,使得对于任意的x1、x2∈[a,b]时,|f(x1)-f(x2)|≤k•|x1-x2|.证明:f(x)为[a,b]上的有界变差函数.
查看习题详情和答案>>
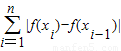 ≤M(i=1,2,…,n)恒成立,则称f(x)为[a,b]上的有界变差函数.
≤M(i=1,2,…,n)恒成立,则称f(x)为[a,b]上的有界变差函数.(1)函数f(x)=x2在[0,1]上是否为有界变差函数?请说明理由;
(2)设函数f(x)是[a,b]上的单调递减函数,证明:f(x)为[a,b]上的有界变差函数;
(3)若定义在[a,b]上的函数f(x)满足:存在常数k,使得对于任意的x1、x2∈[a,b]时,|f(x1)-f(x2)|≤k•|x1-x2|.证明:f(x)为[a,b]上的有界变差函数.
查看习题详情和答案>>
设f(x)是定义在[a,b]上的函数,用分点T:a=x<x1<…<xi-1<xi<…xn=b将区间[a,b]任意划分成n个小区间,如果存在一个常数M>0,使得和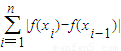 ≤M(i=1,2,…,n)恒成立,则称f(x)为[a,b]上的有界变差函数.
≤M(i=1,2,…,n)恒成立,则称f(x)为[a,b]上的有界变差函数.
(1)函数f(x)=x2在[0,1]上是否为有界变差函数?请说明理由;
(2)设函数f(x)是[a,b]上的单调递减函数,证明:f(x)为[a,b]上的有界变差函数;
(3)若定义在[a,b]上的函数f(x)满足:存在常数k,使得对于任意的x1、x2∈[a,b]时,|f(x1)-f(x2)|≤k•|x1-x2|.证明:f(x)为[a,b]上的有界变差函数.
查看习题详情和答案>>
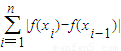 ≤M(i=1,2,…,n)恒成立,则称f(x)为[a,b]上的有界变差函数.
≤M(i=1,2,…,n)恒成立,则称f(x)为[a,b]上的有界变差函数.(1)函数f(x)=x2在[0,1]上是否为有界变差函数?请说明理由;
(2)设函数f(x)是[a,b]上的单调递减函数,证明:f(x)为[a,b]上的有界变差函数;
(3)若定义在[a,b]上的函数f(x)满足:存在常数k,使得对于任意的x1、x2∈[a,b]时,|f(x1)-f(x2)|≤k•|x1-x2|.证明:f(x)为[a,b]上的有界变差函数.
查看习题详情和答案>>
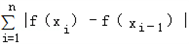 ≤M(i=1,2,…,n)恒成立,
≤M(i=1,2,…,n)恒成立, |x1﹣x2|.证明:f(x)为[a,b]上的有界变差函数.
|x1﹣x2|.证明:f(x)为[a,b]上的有界变差函数.