摘要:求证:an+1+(a+1)2n-1能被a2+a-1整除.分析 数学归纳法可以证明与正整数n有关的命题,常见的恒等式.不等式的命题可用数学归纳法证明,其他的如整除.几何方面的命题也可用数学归纳法证明.在证明n=k+1时,“配凑 的技巧掌握很重要,要有目的去“配凑 倍数式子,以及假设n=k时的式子.证明 (1)当n=1时,a2+(a+1)=a2+a+1可被a2+a+1整除;时,ak+1+(a+1)2k-1能被a2+a+1整除, 2分则当n=k+1时,ak+2+(a+1)2k+1=a?ak+1+(a+1)2(a+1)2k-1=a?ak+1+a?(a+1)2k-1+(a2+a+1)(a+1)2k-1 5分=a[ak+1+(a+1)2k-1]+(a2+a+1)(a+1)2k-1,由假设可知a[ak+1+(a+1)2k-1]能被a2+a+1整除.∴ak+2+(a+1)2k+1也能被a2+a+1整除, 7分即n=k+1时命题也成立.∴对n∈N*原命题成立. 8分
网址:http://m.1010jiajiao.com/timu_id_15716[举报]
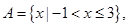
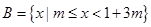
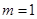 时,求
时,求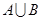 ;
;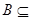
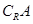 ,求实数
,求实数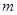 的取值范围.
的取值范围. .
. ,求实数
,求实数 的值;
的值;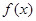 在区间
在区间 上是单调的,求实数
上是单调的,求实数 时,求函数
时,求函数 .
.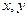 满足
满足 ,求下列各式的最小值,
,求下列各式的最小值,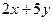 (2)
(2)
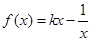 ,且
,且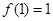 .
. 的值
的值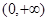 上的单调性;
上的单调性;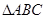 中,
中,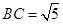 ,
,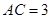 ,
,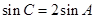 .
.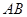 的值;
的值;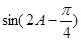 的值.
的值.