摘要:分析 ξ~B(n,p)为二项分布,要熟记二项分布的公式P=pk(1-p)n-k,求P的最大值,还要注意对不等式组的运算.解 ∵ξ服从二项分布,
网址:http://m.1010jiajiao.com/timu_id_14952[举报]
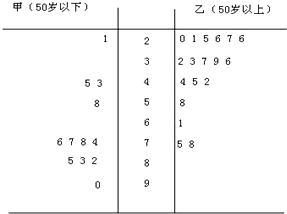 某单位对其员工30人的饮食习惯进行了一次调查,并且用茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主,饮食指数高于70的人,以肉类为主)
某单位对其员工30人的饮食习惯进行了一次调查,并且用茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主,饮食指数高于70的人,以肉类为主)附:K2=
| n(ad-bc)2 |
| (a+d)(c+d)(a+c)(b+d) |
| P(K2≥ko) | 0.25 | 0.15 | 0.10 | 0.05 | 0.024 | 0.010 | 0.005 | 0.001 |
| ko | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(2)根据以上数据完成下列2×2的列联表;
| 主食蔬菜 | 主食肉类 | 合计 | |
| 50岁以下 | 4 4 |
8 8 |
12 12 |
| 50岁以上 | 16 16 |
2 2 |
18 18 |
| 合计 | 20 20 |
10 10 |
30 30 |
某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A、B两种不同的教学方式分别在甲、乙两个班级进行教改实验.为了解教学效果,期末考试后,陈老师甲、乙两个班级的学生成绩进行统计分析,画出频率分布直方图(如图).记成绩不低于90分者为“成绩优秀”.
(1)从乙班随机抽取2名学生的成绩,记“成绩优秀”的个数为ξ,求ξ的分布列和数学期望;
(2)根据频率分布直方图填写下面2×2列联表,并判断是否有95%的把握认为:“成绩优秀”与教学方式有关
附:K2=
查看习题详情和答案>>

(1)从乙班随机抽取2名学生的成绩,记“成绩优秀”的个数为ξ,求ξ的分布列和数学期望;
(2)根据频率分布直方图填写下面2×2列联表,并判断是否有95%的把握认为:“成绩优秀”与教学方式有关
| 甲班(A方式) | 乙班(B方式) | 总计 | |
| 成绩优秀 | |||
| 成绩不优秀 | |||
| 总计 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P≥(k2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 1.323 | 2.072 | 2.706 | 3.814 | 5.024 |
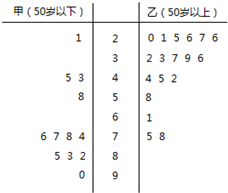 某学生对其亲属30人的饮食习惯进行了一次调查,并用茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主,饮食指数高于70的人,饮食以肉类为主.)
某学生对其亲属30人的饮食习惯进行了一次调查,并用茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主,饮食指数高于70的人,饮食以肉类为主.)(Ⅰ)根据茎叶图,帮助这位学生说明其亲属30人的饮食习惯;
(Ⅱ)根据以上数据完成下列2×2的列联表;
| 主食蔬菜 | 主食肉类 | 合计 | |
| 50岁以下 | |||
| 50岁以上 | |||
| 合计 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,其中学习积极性高的同学中,积极参加班级工作的有18名,不太主动参加班级工作的有7名;学习积极性一般的同学中,积极参加班级工作的有6名,不太主动参加班级工作的有19名.
(Ⅰ)根据以上数据建立一个2×2的列联表;
(Ⅱ)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关系?
参考公式:K2统计量的表达式是:K2=
查看习题详情和答案>>
(Ⅰ)根据以上数据建立一个2×2的列联表;
(Ⅱ)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关系?
参考公式:K2统计量的表达式是:K2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
某校为了探索一种新的教学模式,进行了一项课题实验,乙班为实验班,
甲班为对比班,甲乙两班的人数均为50人,一年后两班进行测试,成绩如下表(总分:150分);
甲班
乙班
(1)现从甲班成绩位于[90,120)内的试卷中抽取9份进行试卷分析,请问用什么抽样方法更合理,并写出最后的抽样结果;
(2)完成下面2×2列联表,你能有97.5%的把握认为“这两个班在这次测试中成绩的差异与实施课题实验有关”吗?并说明理由.
附:
参考公式:K2=
.
查看习题详情和答案>>
甲班为对比班,甲乙两班的人数均为50人,一年后两班进行测试,成绩如下表(总分:150分);
甲班
| 成绩 | [80,90) | [90,100) | [100,110) | [110,120) | [120,130) |
| 频数 | 4 | 20 | 15 | 10 | 1 |
| 成绩 | [80,90) | [90,100) | [100,110) | [110,120) | [120,130) |
| 频数 | 1 | 11 | 23 | 13 | 2 |
(2)完成下面2×2列联表,你能有97.5%的把握认为“这两个班在这次测试中成绩的差异与实施课题实验有关”吗?并说明理由.
| 成绩小于100 | 成绩不小于100分 | 合计 | |
| 甲班 | 50 | ||
| 乙班 | 50 | ||
| 合计 | 36 | 64 | 100 |
| p(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |