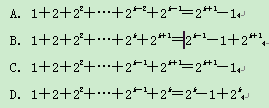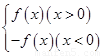摘要：≥×2n-1＝.当且仅当＝1时.等号成立. ----4分 (3)由于＝1.当≥1时.≥. 于是.要使得ST＞2008.只需＞2007. 将按照第一组21项.第二组22项.--.第组项的方式分组.--6分 由(2)可知.每一组的和不小于.且只有＝1时等于. 将这样的分组连续取2×2007组.加上a1.共有24015项. 这24015项之和一定大于1+2007＝2008. 故只需取＝24015,就能使得＞2008, ----8分 (注:只要取出的不小于24015.并说出相应理由.都给满分) (4)设这样的存在. ＝2时.有1＝Þ. ＝3时.有＝Þ.
网址：http://m.1010jiajiao.com/timu_id_148924[举报]
9、设a1，a2，…，a2n+1均为整数，性质P为：对a1，a2，…，a2n+1中任意2n个数，存在一种分法可将其分为两组，每组n个数，使得两组所有元素的和相等求证：a1，a2，…，a2n+1全部相等当且仅当a1，a2，…，a2n+1具有性质P．
查看习题详情和答案>>
已知函数g(x)＝ax3＋bx2＋cx(a∈R且a≠0)，g(－1)＝0，且g(x)的导函数f(x)满足f(0)f(1)≤0.设x1、x2为方程f(x)＝0的两根．
(1)求
的取值范围；
(2)若当|x1－x2|最小时，g(x)的极大值比极小值大
，求g(x)的解析式．
