摘要:(II)解:设求点C到平面ABD的距离为d.于是由(I)结论可知DA⊥平面ABC.∴DA是三棱锥D―ABC的高
网址:http://m.1010jiajiao.com/timu_id_13607[举报]
网址:http://m.1010jiajiao.com/timu_id_13607[举报]
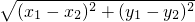 .例如:若
.例如:若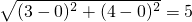 .
.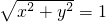 ,即x2+y2=1成立;反过来,如果点P(x,y)的坐标满足等式x2+y2=1,那么点P必在⊙O上,这时,我们就把等式x2+y2=1称为⊙O的方程.
,即x2+y2=1成立;反过来,如果点P(x,y)的坐标满足等式x2+y2=1,那么点P必在⊙O上,这时,我们就把等式x2+y2=1称为⊙O的方程.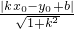 .
. 的距离.
的距离. ,其中n≠0,m>0.
,其中n≠0,m>0.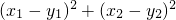 是与n无关的常数,并求出这个常数.
是与n无关的常数,并求出这个常数.