摘要:例5.在中...若以.为焦点的椭圆经过点.则该椭圆的离心率 .
网址:http://m.1010jiajiao.com/timu_id_130200[举报]
1. 构造向量 ,
, ,所以
,所以 ,
, .由数量积的性质
.由数量积的性质 ,得
,得 ,即
,即 的最大值为2.
的最大值为2.
2. ∵ ,令
,令 得
得 ,所以
,所以 ,当
,当 时,
时, ,当
,当 时,
时, ,所以当
,所以当 时,
时, .
.
3.∵ ,∴
,∴ ,
, ,又
,又 ,∴
,∴ ,则
,则 ,所以周期
,所以周期 .作出
.作出 在
在 上的图象知:若
上的图象知:若 ,满足条件的
,满足条件的 (
( )存在,且
)存在,且 ,
, 关于直线
关于直线 对称,
对称, ,
, 关于直线
关于直线 对称,∴
对称,∴ ;若
;若 ,满足条件的
,满足条件的 (
( )存在,且
)存在,且 ,
, 关于直线
关于直线 对称,
对称, ,
, 关于直线
关于直线 对称,
对称,
 ∴
∴ .
.
4. 不等式 (
( )表示的区域是如图所示的菱形的内部,
)表示的区域是如图所示的菱形的内部,
∵
 ,
,
当 ,点
,点 到点
到点 的距离最大,此时
的距离最大,此时 的最大值为
的最大值为 ;
;
当 ,点
,点 到点
到点 的距离最大,此时
的距离最大,此时 的最大值为3.
的最大值为3.
5. 由于已有两人分别抽到5和14两张卡片,则另外两人只需从剩下的18张卡片中抽取,共有 种情况.抽到5 和14的两人在同一组,有两种情况:
种情况.抽到5 和14的两人在同一组,有两种情况:
(1) 5 和14 为较小两数,则另两人需从15~20这6张中各抽1张,有 种情况;
种情况;
(2) 5 和14 为较大两数,则另两人需从1~4这4张中各抽1张,有 种情况.
种情况.
于是,抽到5 和14 两张卡片的两人在同一组的概率为 .
.
 6. ∵
6. ∵ ,∴
,∴ ,
,
设 ,
, ,则
,则 .
.
作出该不等式组表示的平面区域(图中的阴影部分 ).
).
令 ,则
,则 ,它表示斜率为
,它表示斜率为 的一组平行直线,易知,当它经过点
的一组平行直线,易知,当它经过点 时,
时, 取得最小值.
取得最小值.
解方程组 ,得
,得 ,∴
,∴
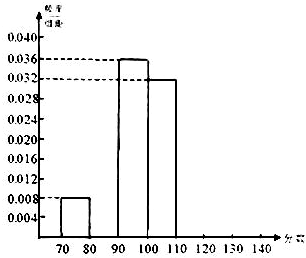 从某校参加2009年全国高中数学联赛预赛的450名同学中,随机抽取若干名同学,将他们的成绩制成频率分布表,下面给出了此表中部分数据.
从某校参加2009年全国高中数学联赛预赛的450名同学中,随机抽取若干名同学,将他们的成绩制成频率分布表,下面给出了此表中部分数据.(1)根据表中已知数据,你认为在①、②、③处的数值分别为
(2)补全在区间[70,140]上的频率分布直方图;
(3)若成绩不低于110分的同学能参加决赛,那么可以估计该校大约有多少学生能参加决赛?
| 分组 | 频数 | 频率 |
| [70,80) | 0.08 | |
| [80,90) | ③ | |
| [90,100) | 0.36 | |
| [100,110) | 16 | 0.32 |
| [110,120) | 0.08 | |
| [120,130) | 2 | ② |
| [130,140] | 0.02 | |
| 合计 | ① |
 从某校参加2009年全国高中数学联赛预赛的450名同学中,随机抽取若干名同学,将他们的成绩制成频率分布表,下面给出了此表中部分数据.
从某校参加2009年全国高中数学联赛预赛的450名同学中,随机抽取若干名同学,将他们的成绩制成频率分布表,下面给出了此表中部分数据.(1)根据表中已知数据,你认为在①、②、③处的数值分别为______,______,______.
(2)补全在区间[70,140]上的频率分布直方图;
(3)若成绩不低于110分的同学能参加决赛,那么可以估计该校大约有多少学生能参加决赛?
| 分组 | 频数 | 频率 |
| [70,80) | 0.08 | |
| [80,90) | ③ | |
| [90,100) | 0.36 | |
| [100,110) | 16 | 0.32 |
| [110,120) | 0.08 | |
| [120,130) | 2 | ② |
| [130,140] | 0.02 | |
| 合计 | ① |
查看习题详情和答案>>
 从某校参加2009年全国高中数学联赛预赛的450名同学中,随机抽取若干名同学,将他们的成绩制成频率分布表,下面给出了此表中部分数据.
从某校参加2009年全国高中数学联赛预赛的450名同学中,随机抽取若干名同学,将他们的成绩制成频率分布表,下面给出了此表中部分数据.(1)根据表中已知数据,你认为在①、②、③处的数值分别为______,______,______.
(2)补全在区间[70,140]上的频率分布直方图;
(3)若成绩不低于110分的同学能参加决赛,那么可以估计该校大约有多少学生能参加决赛?
| 分组 | 频数 | 频率 |
| [70,80) | 0.08 | |
| [80,90) | ③ | |
| [90,100) | 0.36 | |
| [100,110) | 16 | 0.32 |
| [110,120) | 0.08 | |
| [120,130) | 2 | ② |
| [130,140] | 0.02 | |
| 合计 | ① |
查看习题详情和答案>>